基于压缩空气储能附加阻尼控制的电力系统低频振荡抑制策略-中国储能网

中国储能网讯：随着电力系统中电力电子设备的渗透率大幅提升，在扰动下系统发生低频振荡失稳问题日益凸显。为此，结合压缩空气储能良好的有功调节能力，提出了抑制电网低频振荡的压缩空气储能附加阻尼控制方法。首先，建立了压缩空气储能的数学模型，分析了质量流量对其输出功率的影响。其次，分析压缩空气储能抑制低频振荡的可行性，提出了基于调节阀的附加阻尼控制器，调整质量流量，进而控制压缩空气储能的输出功率，抑制电网的低频振荡。最后，搭建含压缩空气储能的4机2区域电力系统仿真模型，验证所提方法的有效性。仿真结果显示所提方法能够为电网提供正阻尼，可较快抑制电网的低频振荡，有效提高电力系统的稳定性。

01、压缩空气储能数学模型

CAES系统包含压缩机、透平机、换热器和储气库等，本文对CAES的释能环节进行研究，不涉及储能环节，因此只建立释能过程的数学模型。图1为典型的三级透平CAES的释能结构。CAES释能时，通过调整调节阀的开度L，控制储气库中压缩气体的流量，进入换热器加热，并通过透平机做功实现系统的发电。

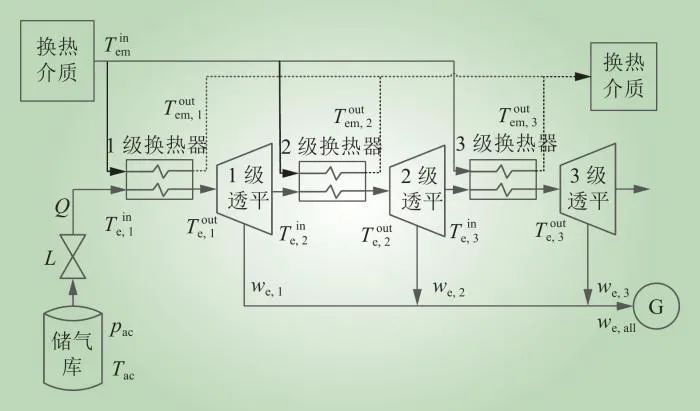
图1 CAES释能过程示意

Fig.1 Energy release process of CAES

1）储气库模型。

设CAES储气库储存高压气体为定容过程，空气为理想状态。根据质量和能量守恒定律，释能阶段储气库内压力和温度的变化趋势表达式为

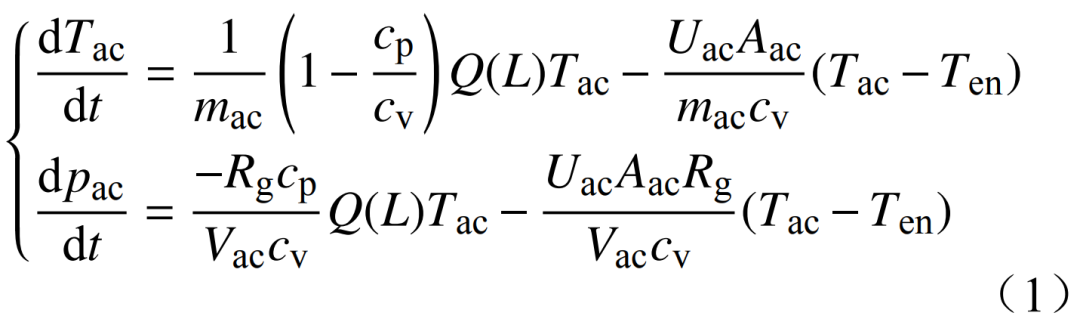
式中：T_ac、p_ac、V_ac分别为储气库内部的温度、压力和体积；m_ac为储气库内的空气质量；c_p、c_v、R_g为理想空气状态的参数；U_ac为储气库与环境的传热系数；A_ac为储气库内的面积；T_en为环境温度；Q(L)为调节阀开度L下的质量流量。

2）调节阀模型。

假设CAES输出额定功率下质量流量Q(L)仅与调节阀开度L有关，利用百分比表示阀门的开度，此时调节阀开度和质量流量之间的关系可近似表示为指数函数，如式（2）所示，质量流量和阀门开度的关系如图2所示。

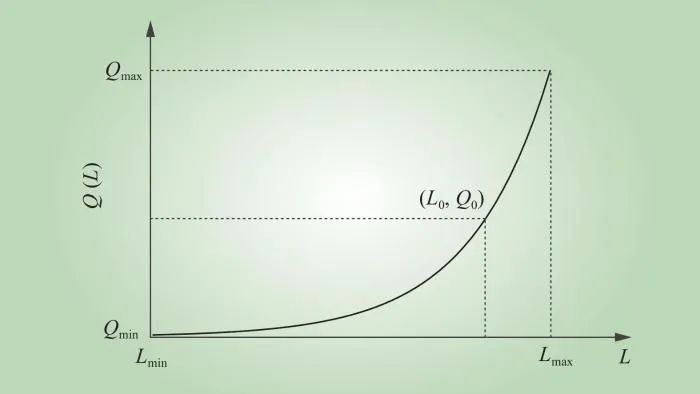
图2 调节阀开度和质量流量关系

Fig.2 Relationship between valve opening and mass flow

式中：Q_max为调节阀的最大质量流量；L_max为调节阀的最大开度；R为最大质量流量和最小质量流量之比。

调节阀开度执行机构的传递函数为

式中：T_m为时间常数；µ为调节阀开度执行机构的控制信号。

3）换热器模型。

释能时，每一级换热器回热后的空气温度为

式中：i表示透平级数；

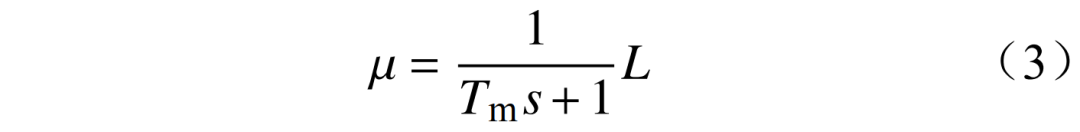
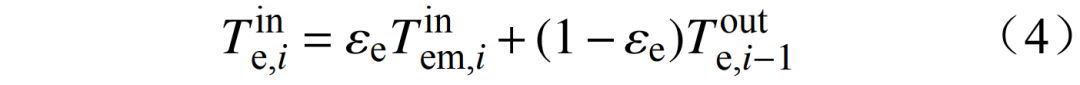
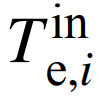为每一级换热器的输入温度；

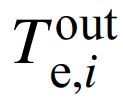为每一级换热器的空气输出温度；

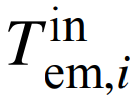为每一级换热器的热介质的输入温度；ε_e为换热器的换热效率，其为常数。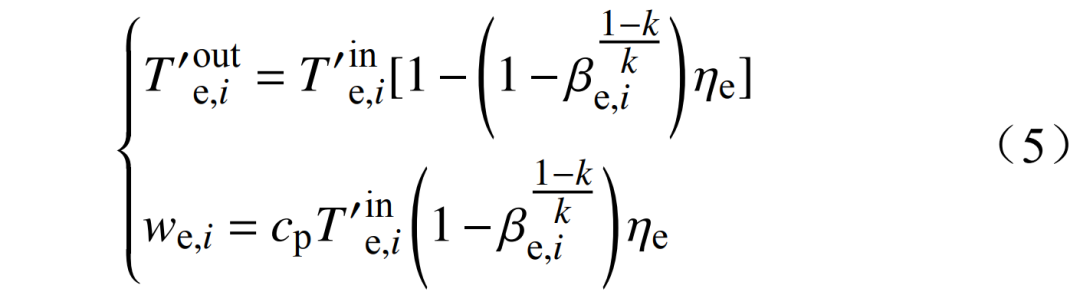

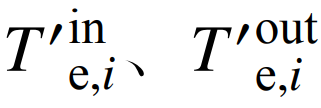4）透平机模型。

透平机出口空气温度和单位质量空气经透平机做功表达式为

式中：

分别为透平机的空气输入温度、输出温度，即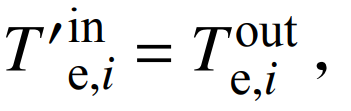

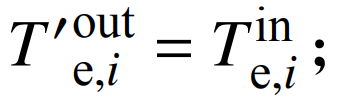k为理想空气比热容；β_e,i为每一级的膨胀比；η_e为透平机效率。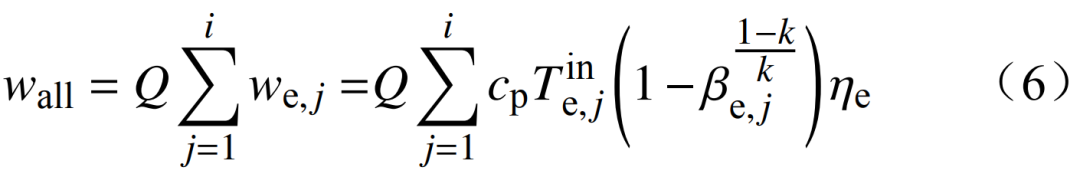

CAES的输出功率表达式为

式（6）中，若c_p、

β_e,j、k、η_e为常数时，单位空气质量流量下透平机做功的总量w_all为常数。因此，c_p、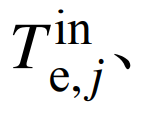

β_e,j、k、η_e为常数时，CAES输出功率与质量流量呈线性关系，即通过调节阀开度来调整质量流量，进而调整透平机的总功率。

综上所述，通过建立储气库内压力和温度变化的模型，保障CAES抑制电网低频振荡时储气库的安全稳定，并以此作为压缩空气储能的附加阻尼控制器参数取值的约束条件，保证参数取值的合理性；其次，通过调节阀开度与质量流量间近似等于指数函数的特性曲线、质量流量与输出功率间的线性关系，提出压缩空气储能抑制低频振荡的控制架构，同时通过建立换热器温度变化的模型，保障透平机稳定输出所需的功率。

02、基于CAES附加阻尼的电力系统低频振荡调控策略

2.1 CAES抑制电力系统低频振荡的可行性分析

含CAES的两区域等值二机系统如图3所示。图3中，X₁∼X₃为线路电抗；E₁∠δ、E₂∠0°、E₃∠(δ−θ)分别为母线1、母线2、母线3的电压；P_C、P₁、P₂分别为CAES输出功率、母线1向母线3传输的功率、母线2向母线4传输的功率；设母线2的电压E₂∠0°为参考电压。

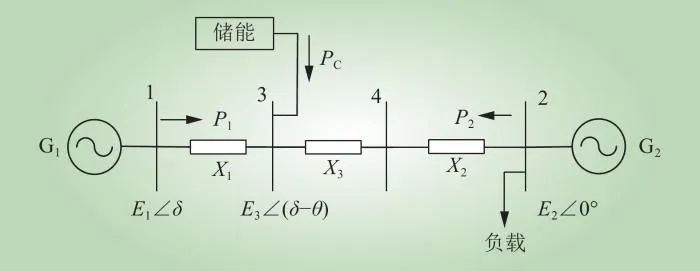
图3 含CAES的电力系统

Fig.3 The power system with CAES

小扰动下电力系统发生低频振荡，引起同步发电机的电磁功率发生变化，并破坏同步发电机的机械转矩和电磁转矩之间的平衡，进而使同步发电机发生功角振荡。采用经典2阶动态方程，且在工作点附近线性化后，低频振荡下功率变化量为

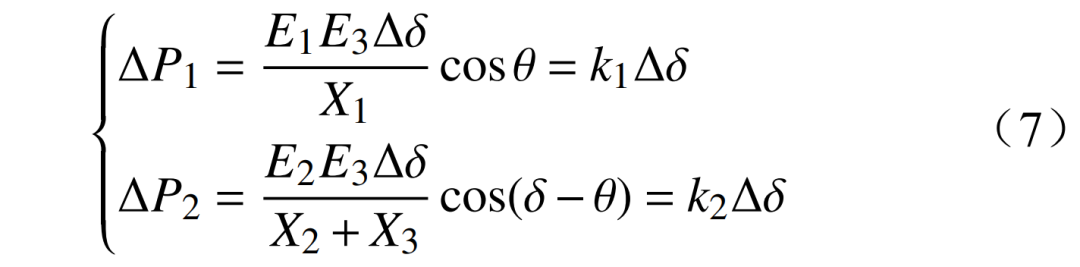
式中：∆P₁、∆P₂分别为母线1与母线3之间的功率增量和母线2与母线4之间的功率增量；δ为初始时刻的功角；θ为初始时刻母线1和母线3之间的相角偏差；∆δ为功角振荡的变化量；k₁，k₂分别为调节系数。

电力系统发生低频振荡时，CAES向母线3输入有功功率进行调节，确保系统稳定。此时，CAES有功功率用角速度表示为

式中：∆P_C为CAES的有功功率增量；k_p为调节系数；∆ω_r为角频率变化率。

根据功率平衡关系，小扰动下发电机的转子运动方程的增量可表示为

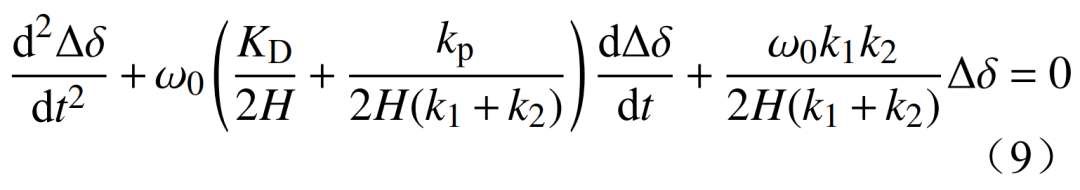
式中：K_D为阻尼系数；H为惯性时间常数；ω₀为初始角速度。

由式（9）可知，系统的阻尼比ξ为

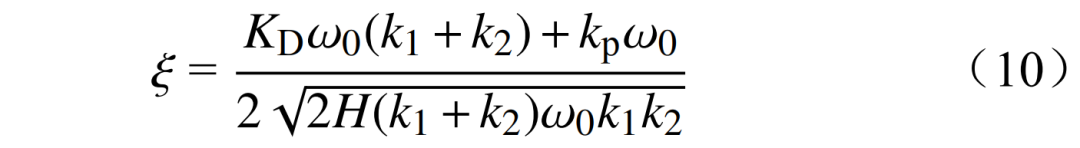
当k_p/ (k₁+k₂)k_p>0时，系统阻尼表现为正阻尼，若通过增大CAES的参数k_p，可增大系统的阻尼，有助于CAES抑制电力系统的低频振荡。因此，通过CAES抑制电力系统的低频振荡是可行的。

2.2 压缩空气储能的附加阻尼控制

为了有效提高CAES抑制电力系统低频振荡的能力，提出了调节阀的附加阻尼控制器，其控制框图如图4所示。附加阻尼控制器中包括增益环节、滤波环节、相位补偿环节和限幅环节。

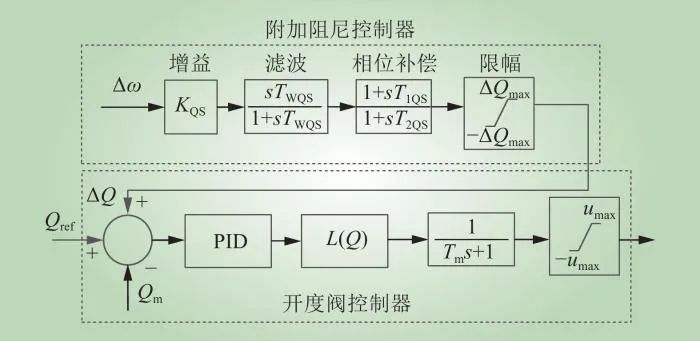
图4 调节阀的附加阻尼控制器结构

Fig.4 The supplementary damping controller structure of regulating valve

附加阻尼控制器中的增益环节调节信号的大小，滤波环节消除特定频段以外的信号，相位补偿环节调整信号的相位，限幅环节剔除超过附加控制信号上下限的值，防止超调。当电力系统频率发生低频振荡时，转速差增量

经过附加阻尼控制器获得附加控制信号，动态调整质量流量，控制CAES的输出功率。附加阻尼控制器的传递函数表达式为

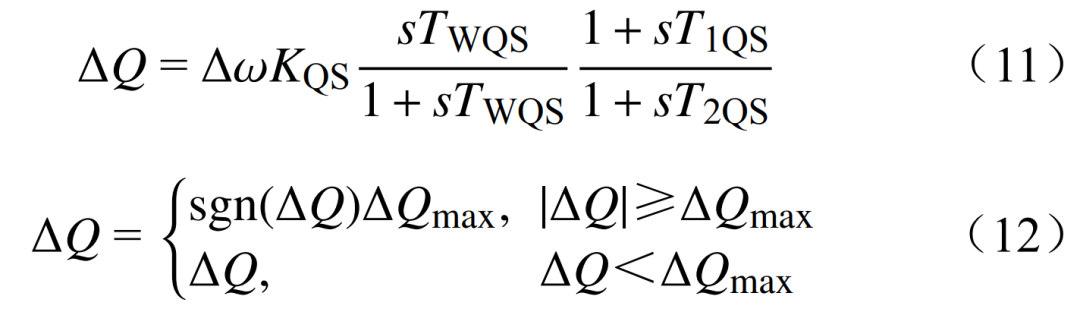
式中：K_QS、T_WQS、T_1QS、T_2QS为控制器参数；∆Q为质量流量的调节指令；∆Q_max为附加阻尼控制器输出指令的最大幅值。

CAES输出额定功率时的质量流量Q_ref与实际质量流量的平均值Q_m相减，通过PID控制后得到稳定的质量流量信号，计算获得调节阀开度的信号，最后经过惯性环节和限幅环节后得到开度信号，调整调节阀的开度，进而控制质量流量。

电力系统发生低频振荡时，通过转速差增量∆ω调整CAES质量流量，并通过透平输出功率P与质量流量Q之间的线性关系获得功率增量∆P，调整透平输出功率，驱动CAES的同步发电机输出有功功率，抑制电力系统低频振荡，增强电力系统阻尼，提升电力系统的稳定性。为了保障压缩空气储能安全稳定运行，且合理地设置附加阻尼控制器的参数，将储气库的温度和压强、调节阀的最大开度、调节阀的最大质量流量等作为约束条件，使CAES的参数k_p＞0且电力系统可安全稳定运行时，阻尼控制器设置合理的控制参数即可。

03、仿真分析

3.1 参数设置

采用经典的4机2区域电力系统模型，验证所提控制策略的有效性。4机2区域电力系统拓扑结构如图5所示，CAES系统通过升压变压器接入母线7，CAES系统输出电压为10 kV，额定容量为100 MV·A，母线7的额定电压为230 kV，G₁~G₄为4台额定容量均为700 MV·A的同步发电机，发电机的额定电压为20 kV。CAES系统参数如表1和表2所示，附加阻尼控制器参数如表3所示。为模拟弱阻尼系统，发电机G2的惯性常数设置为10，开启G1的PSS控制器，关闭G2、G3、G4发电机的PSS控制器，避免系统因阻尼不足而解列。系统启动时发生减幅振荡模式的低频振荡，下面分析CAES有无附加阻尼控制下各状态量的变化。

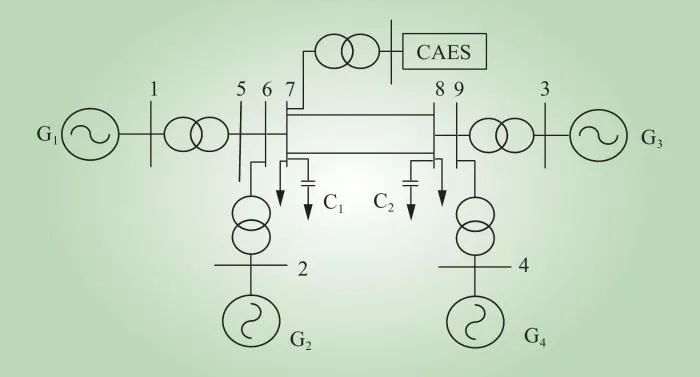
图5 含CAES的4机2区域电力系统

Fig.5 The power system of 4-generator and 2-area with CAES

表1 CAES系统的参数

Table 1 Parameters of CAES system

表2 CAES同步发电机的参数

Table 2 Parameters of CAES synchronous generator

表3加阻尼控制器的参数

Table 3 Parameters of additional damping controller

3.2 仿真结果

由图6可知，CAES无附加阻尼控制时，初始时刻线路的传输功率发生衰减振荡模式的低频振荡，在90 s时，传输功率仍然发生较小的振荡，降低了系统的稳定性。CAES采用附加阻尼控制时，传输功率在35 s左右停止振荡，有效提升系统的稳定性。可见，CAES采用附加阻尼控制后，可在较短时间内有效抑制传输线路有功功率的低频振荡。

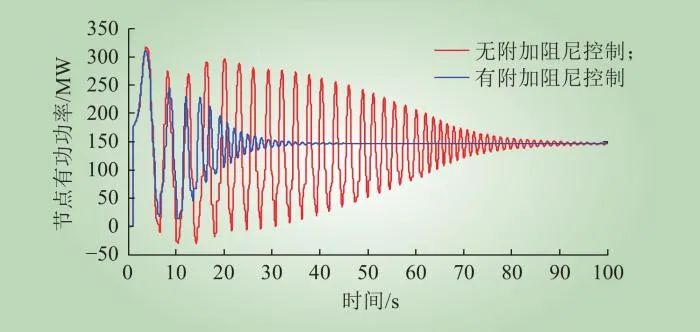
图6 区域间传输线有功功率振荡

Fig.6 Active power oscillation of transmission lines

采用Prony算法分析母线7与母线8之间的线路传输功率的阻尼比，如表4所示。从表4可知，CAES采用附加阻尼后，线路传输功率的阻尼比为0.190，大于CAES无附加阻尼控制的阻尼比0.035。可见，CAES采用附加阻尼控制后增强了4机2区域系统的阻尼，极大提升了系统稳定性。

表4 Prony分析结果

Table 4 Prony analysis results

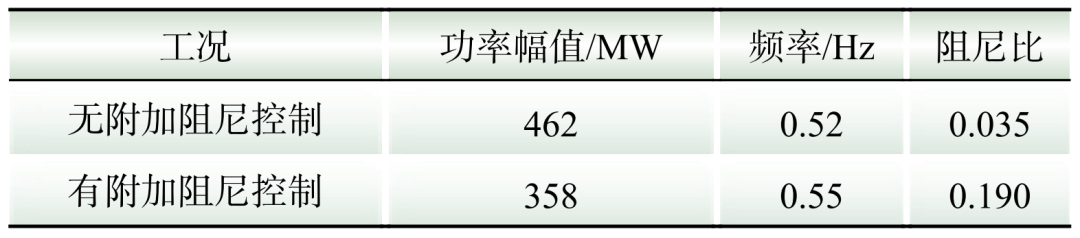
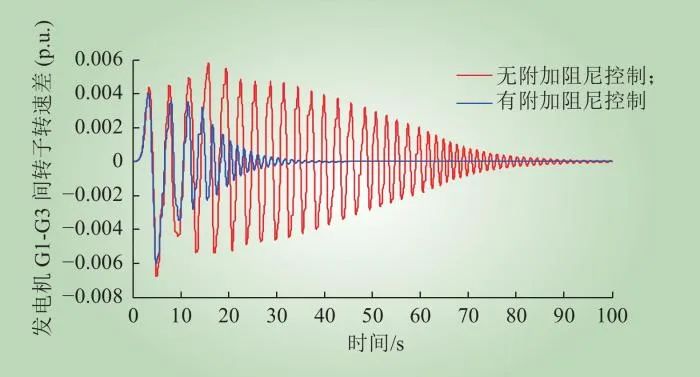
图7 同步发电机G1和G3转速差

Fig.7Rotating difference between synchronous generator G1 and G3

CAES有无附加阻尼控制下，其发电机转子转速、输出有功功率分别如图8、图9所示。从图8可知，CAES无附加阻尼控制中，前10 s时CAES根据电网运行情况调整其出力，10 s后CAES转子转速才发生衰减型的低频振荡，且在90 s时仍然有微小的振荡，不利于系统的稳定；CAES采用附加阻尼控制中，前10 s出力与CAES无附加阻尼控制中相同，且在30 s左右完全抑制了低频振荡，极大提升了电网的稳定性。从图9可知，CAES无附加阻尼控制中，前10 s时CAES根据电网运行情况调整其出力，10 s后CAES输出有功功率发生衰减型的低频振荡，在90 s时也依然有微小的振荡；CAES采用附加阻尼控制后，前10 s出力与CAES无附加阻尼控制中相同，且在35 s左右停止了振荡，有效抑制了功率的振荡。可见，CAES采用附加阻尼控制后，可有效抑制CAES的发电机转子转速和输出有功功率的低频振荡。

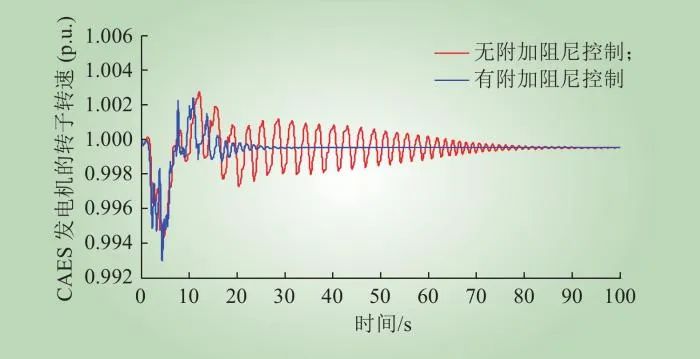
图8 CAES发电机的转子转速

Fig.8 Rotating speed of CAES generator

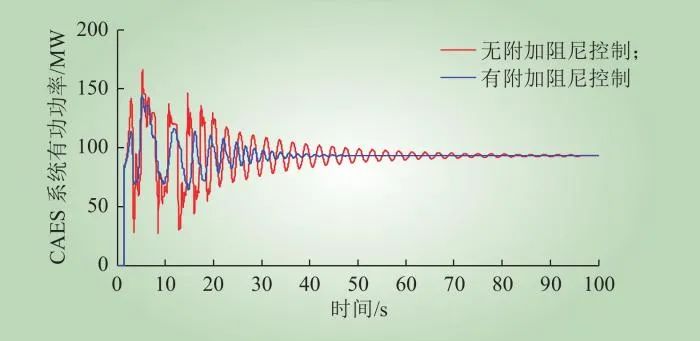
图9 CAES的有功功率

Fig.9 Active power of CAES

CAES有无附加阻尼控制下，CAES透平机的总功率变化趋势如图10所示。由图10可知，CAES无附加阻尼控制时，CAES输出稳定的质量流量，透平机的总输出功率稳定不变；CAES采用附加阻尼控制后，调节阀受附加阻尼信号控制，输出变化的透平功率，质量流量的变化率基本维持在±30%内。可见，CAES采用附加阻尼控制时，质量流量在较小范围内变化，保障了CAES系统的稳定性。

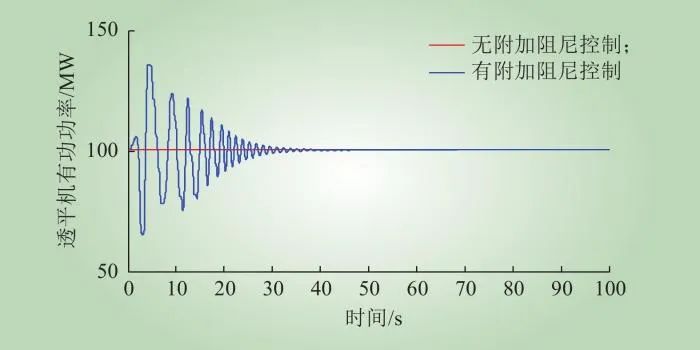
图10CAES透平机的总功率

Fig.10 Total power of CAES turbine system

CAES有无附加阻尼控制下，储气库内部压力和温度的变化情况分别如图11和图12所示。由图11可知，CAES有无附加阻尼控制下，储气库内部压力均在10 s内迅速下降至9.77 MPa，且均在10 s后以0.0012 MPa/s的速度平缓下降。由图12可知，2种控制下，前10 s内储气库内部温度与储气库内部压力变化类似，但储气库内部温度均最终稳定在293 K左右，与CAES采用附加阻尼控制无关。可见，CAES有无附加阻尼控制对储气库内部压力和温度影响较小。

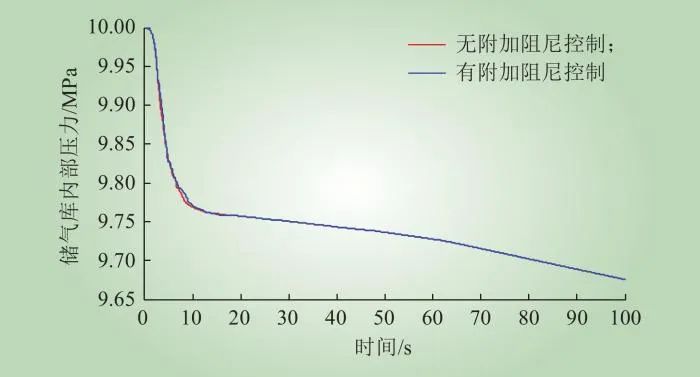
图11 储气库内部压力

Fig.11 Internal pressure of gas storage container

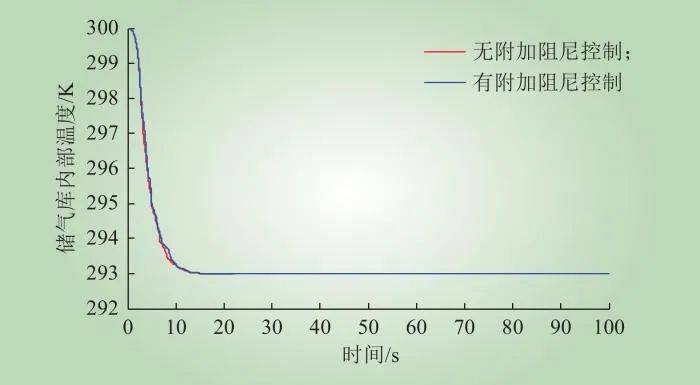
图12 储气库内部温度

Fig.12 Internal temperature of gas storage container

由图8可知，在前10 s时，压缩空气储能需要快速调整其出力，压缩空气储能转子转速须快速进行调整，变化无规律，且通过释能阶段储气库内压力和温度的变化数学模型可知，此时压缩空气储能储气库压力和温度变化较快；而10 s之后压缩空气储能转子转速变化为衰减型的低频振荡，压缩空气储能有功出力已经可以跟随电力系统有功变化，通过释能阶段储气库内压力和温度的变化数学模型可知，压缩空气储能储气库压力和温度变化较慢。可见，CAES储气库内部压力和温度的变化与CAES出力相关，且其变化趋势与分析一致。

04、结论

针对电力系统发生低频振荡问题，提出了抑制电网低频振荡的CAES附加阻尼控制方法，采用含CAES的4机2区域电力系统模型，验证了所提控制策略的有效性，并得到了如下结论。

1）CAES附加阻尼控制方法可有效增大电力系统的阻尼，较大程度缩短振荡的衰减时间，对电力系统低频振荡有显著抑制作用，提升了电力系统运行稳定性。

2）CAES附加阻尼控制方法可使其在较小范围内改变其输出的质量流量和输出功率，保障了CAES系统的稳定性。当储气库内有足够的空气时，CAES采用附加阻尼时，对CAES内部温度和压力的影响较小，储气库内部状态仍能保持稳定，有效保障了CAES系统的稳定性。

【责任编辑:欧阳勇】