中国储能网讯：

　　摘要：微电网由分布式电源、储能装置及本地负载构成，既可并网运行也可孤岛运行。实现2 种运行模态的平滑过渡和切换是其关键技术之一，其中锁相环起到很重要的作用。微网主从控制结构中，主逆变器在并网运行时与电网电压同步，孤岛运行时为从逆变器产生电压参考。本文给出一种提取电网电压正序分量的锁相环模型，可确保微网运行模式的平滑转化，减少切换时的暂态影响，增强了系统的稳定性。最终，基于TMS320F28335 搭建一台原理样机，实验结果表明文中给出的锁相环模型的有效性和可行性。

　　关键词：微网，逆变器，锁相环，正序分量，运行模式切换

　　1.引 言

　　微电网是将分布式电源、储能单元、负荷以及监控、保护装置结合在一起，形成一个对公共电网来说单一可控的单元，同时也向用户提供能量。微网主要有并网和孤岛两种运行模式。在微网的主从控制结构中，并网运行时，主逆变器需要锁定电网相位，实现与公共电网的精确同步;孤岛运行时，主逆变器需要为微网建压，从而为从逆变器提供电压和频率参考。为避免动态切换时产生过大的环流，切换过程必须平稳连续[1]。

　　锁相环需要给微网系统提供相位信息，从而产生电流基准，所以其对微网模式的切换起到关键的作用。目前用于微网的锁相环存在很多不足，文献[2]将三相电压经过Clark 变换得到其α ,β 分量，进而得到其相角值，这种方法对输入电压谐波的抑制作用弱。文献[3]对基于Park 变换的锁相环进行分析，其可以通过调节锁相环的带宽，来获得较强的谐波抑制能力;但当三相电压不平衡时，锁相角输出存在不可消除的2 次谐波，从而降低并网电能质量和系统稳定性。此外，上述锁相方法主要用于微网的并网阶段，无法实现微网不同模式的平滑切换。本文给出一种可提取电网电压正序分量的锁相方法[4]，一方面解决了三相电压不平衡的问题;另一方面在孤岛模式下可自振荡产生固定频率的信号，并且可以在不同工作模式间进行平滑的动态切换[5]。

　　本文首先介绍微网逆变器锁相环的工作原理;其次，对文中给出的锁相环性能进行分析，介绍孤岛下锁相环自振荡原理，并给出相应的数字实现方法;最终，基于F28335 搭建实验平台进行实验验证。

　　2.微网逆变器锁相环工作原理

　　2.1 微网逆变器系统结构

　　微网逆变器结构如图1 所示，包括主逆变器拓扑、控制电路、锁相环及公共电网等部分。

　　逆变器与公共电网之间通过静态开关S 相连。微网不同的工作模式，对应的控制方式不同：并网模式采取单电流环控制，静态开关S 闭合、控制开关DF 断开，此时锁相环跟踪电网相位，并产生电流基准;孤岛模式采取电压外环电流内环的双环控制策略，静态开关S 打开、控制开关DF 闭合，此时逆变器与电网断开连接，锁相环内部自振荡，产生幅值和频率可控的电压信号，为系统提供电压和频率支撑。

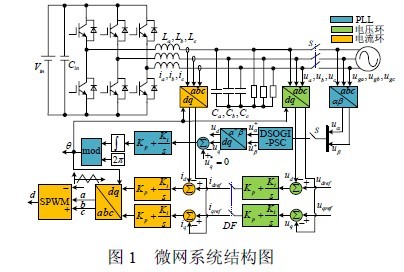
　　2.2 锁相环性能分析

　　锁相环结构如图2 所示。

　　正序分量提取需要两路正交信号，目前，常采用二阶广义积分(Second Order Generalized Integrator，SOGI)算法来构造2 路正交信号。并网运行时，图中控制开关DF 为0，分别对Clark 变换的两路输出信号进行二阶广义积分，从而分别得到其对应的正交信号，再经过后面的PSC 代数运算便可提取出电网电压的正序分量;孤岛运行时DF 为1，幅值控制器输出Camp为系统自振荡提供初始条件，使得孤岛模式下锁相环仍然能够工作。此外，并网运行时，当电网频率发生变化时，为了实现对输入信号相位实时跟踪，需要对谐振频率0ω 进行自适应控制，实时更新0ω 值，该功能由锁频环来实现。

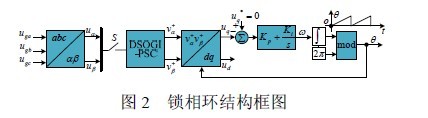
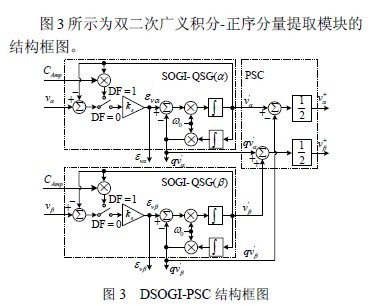
　　3.2 锁频环(FLL)

　　图4 给出了锁频环的结构框图。

　　3.3 幅值控制器

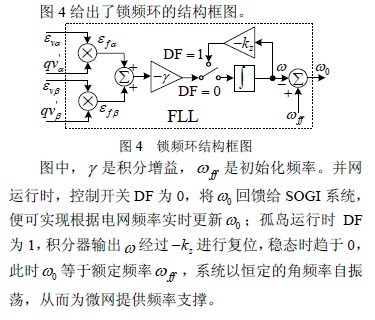
　　系统在孤岛模式下运行时，要想锁相环能够自振荡，必须给其一个初始的振荡条件，且为了使提取的正序信号幅值与逆变器输出电压幅值一致，必须要跟踪孤岛模式下逆变器输出电压基准值，为此本文给出的锁相环系统中增加一个幅值控制器，如图5 所示。

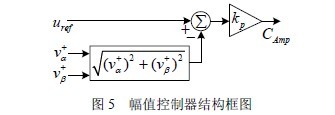
　　并网模式下，幅值控制器不起作用;在孤岛模式下，基准电压与正序信号幅值的差值经过比例控制器回馈给二阶广义积分器，从而构成负反馈，使得正交信号跟踪逆变器输出电压幅值。

　　4.实验结果及分析

　　为了验证本文给出的微网用锁相环的可行性与性能，基于F28335 搭建实验平台。实验参数：开关器件选用SPM IGBT 模块，输入电压280VDC，输出电压110VAC，开关频率18kHz，滤波电感和电容分别为3mH 和10μF。图6 所示为公共连接点(PCC)处三相电压及锁相角波形。

　　当DF 为0 时，提取电网电压正序分量;当DF 为1，由幅值控制器跟踪逆变器输出电压基准，获得逆变器输出电压正序分量。从实验结果可得，切换过程中正序分量能平滑过渡。

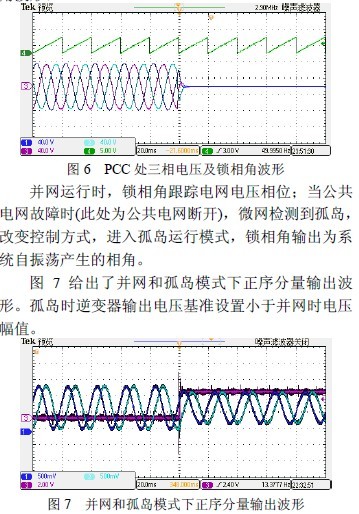
　　图8 给出了并网和孤岛模式下，锁相角输出波形。

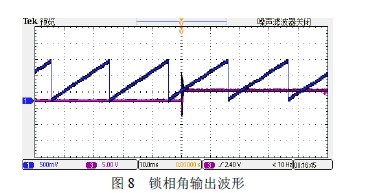
　　从实验结果可以看出，在动态切换过程中，锁相角基本无波动，所以可以实现微网由并网到孤岛模式的平滑无缝切换。

　　5.结 论

　　针对传统锁相环用于微网系统中存在诸多不足，本文给出一种适用于微网系统的锁相环方法，对其性能和各模块进行分析，并给出相应的数字实现方法;最终，基于F28335 搭建实验平台进行实验验证，并得出如下结论：

　　(1) 系统锁频环能够实时跟踪电网角频率的变化;

　　(2) 幅值控制器能够使得正序分量在孤岛模式下

　　跟踪逆变器输出电压基准;

　　(3) 在模式切换过程中，文中给出的锁相环动态响

　　应快且可以实现平滑无缝切换。

　　参考文献

　　[1] 王成山,杨占刚,王守相,车延博. 微网实验系统结构特征

　　及控制模式分析[J]. 电力系统自动化, 2010 ，

　　34(1):99-105.

　　[2] M. Karimi-Ghartemani, M. R. Iravani, “A method for

　　synchronization of power electronic converters in polluted

　　and variable-frequency environments,” IEEE Trans. on

　　Power Systems, vol. 19, pp. 1263-1270, 2004.

　　[3] Chung S, “A phase tracking system for three phase utility

　　interface inverters,” IEEE Trans. on Power Electronics,

　　vol. 15, no. 3, pp. 431-438, 2000.

　　[4] P. Rodríguez, A. Luna, I. Candela, R. Teodorescu, and F.

　　Blaabjerg, “Grid synchronization of power converters

　　using multiple second order generalized integrators, ”

　　IECON 2008. 34th Annual Conference of IEEE.

　　[5] Gustavo M. S. Azevedo, Marcelo C. Cavalcanti, Fabricio

　　Bradaschia, Joan Rocabert, Francisco A. S. Neves, “Safe

　　transient operation of microgrids based on master-slave

　　configuration,” Energy Conversion Congress and