本文引文信息

伍俊, 鲁宗相, 乔颖, 等. 考虑储能动态充放电效率特性的风储电站运行优化 [J]. 电力系统自动化, 2018, 42(11): 41-47. DOI: 10.7500/ AEPS20180326002.

WU Jun, LU Zongxiang, QIAO Ying, et al. Optimal Operation of Wind Farm with Hybrid Storage Devices Considering Efficiency Characteristics of Dynamic Charging and Discharging [J]. Automation of Electric Power Systems, 2018, 42(11): 41-47. DOI: 10.7500/ AEPS20180326002.

考虑储能动态充放电效率特性的风储电站运行优化

DOI: 10.7500/AEPS20180326002

伍俊，鲁宗相，乔颖，杨海晶

1、研究背景

近年来，中国新能源迅猛发展，但同时弃风弃光矛盾凸显，风电场与储能联合是提升风电场消纳的有效途径。储能效率直接影响风储联合发电系统的消纳效果，但目前的常数效率模型对储能的效率特性刻画不够精细。本文以等效风电消纳量最大为目标，建立了考虑储能动态效率的风电储能联合发电系统运行优化模型。该模型考虑了储能在充放电运行功率不同时的效率变化，将动态效率以分段函数形式纳入混合整数线性优化模型。基于实际风电场运行数据进行了仿真分析，证明了动态效率特性对最大化消纳具有显著影响，是风储联合系统运行优化值得纳入考虑的因素。

2、储能的动态效率特性

不同的储能设备，其运行功率范围、效率大小、动态效率变化的快慢程度不同，难以直接比较分析，为统一考虑其动态充放电特性，采用功率-效率曲线来描述。某先进绝热压缩空气储能发电设备透平机的效率随功率的变化为一条“上升”曲线，发电环节效率可认为透平发电设备的效率和包括储热设备在内的其他环节效率的乘积，得到整个发电环节的效率变化如图1，是一种“上升型”的特征。

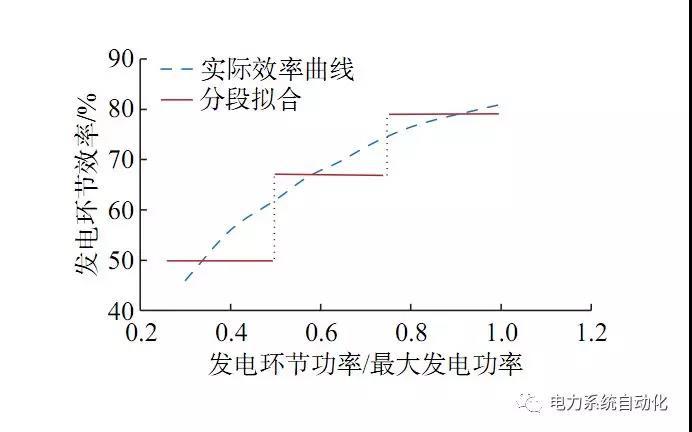
图1  主储能发电部分的分段功率-效率曲线

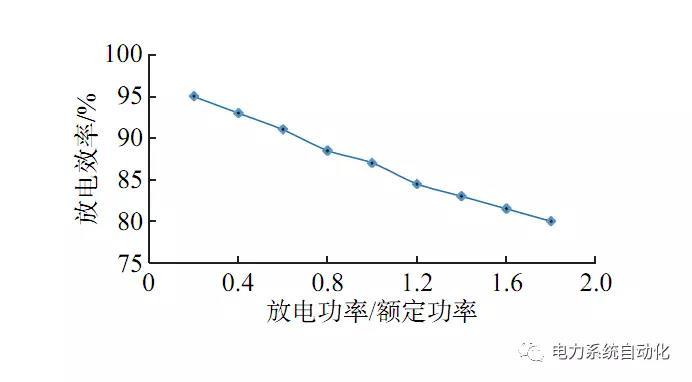
图2  锂电池放电功率-效率曲线

电化学储能的效率特性与压缩空气储能完全不同。以放电环节为例，铅酸电池和锂电池储能在合理放电深度范围（典型值SOC在20%~95%区间），电压基本不变，效率随着放电电流的增大有不同程度的降低。依据锂电池放电深度与电压的关系、放电效率与电流的关系得到锂电池放电效率变化特性，有着“下降型”特征，且近似线性。

3、风储联合运行优化模型

风储联合运行优化模型目标函数为最大化风电的等效消纳量，包括三个部分：一段时间内直接上网电量、储能系统中的未上网电量变化额、运行过程中的耗能（如冷启动消耗、热备用状态的消耗，包括辅机、储热装置消耗等）。

考虑到效率随功率变化而变化，电量为功率的积分函数，呈现为非线性形式，与电量相关的目标函数与约束条件均会非线性化，为了综合考虑模型求解的复杂度和最优解的可靠性，用分段函数来拟合动态效率曲线，储能功率由一组连续变量和0-1变量表示，从而使得包括储能的功率约束、电量上下限约束、启停约束等在内的约束条件线性化，目标函数也表示为变量的线性函数，该优化模型转化为线性混合整数规划，易于求解。

4、算例分析

主储能放电的功率范围取30%-100%，功率均匀划分三段，即n=3，效率取值不均匀以保留曲线的非线性变化特征，三段效率取值为0.5、0.68、0.8，充电环节类似。

4.1  只接入主储能时的不同效率模型消纳效果分析

1）放电时段

在动态效率模型下，其特性是放电功率小对应效率低，放电功率大对应效率高，因此，不同放电功率下的等效消纳电量不同，放电功率越低则消纳电量越小，放电过程中损失的能量越大。图3给出了主储能放电时段的A、B两种极限情况，B以最大功率即对应最高效率放电，可释放能量的等效消纳电量最大；而A的放电功率及对应效率最低，更多的能量被损耗，等效消纳电量最小，B工况即为考虑动态效率模型下的最优结果。常数、动态模型的消纳效果最大差异值即为A、B工况的差值，相对差值为34.74%，一般常数效率取效率曲线的平均值，其消纳差异会小一些。

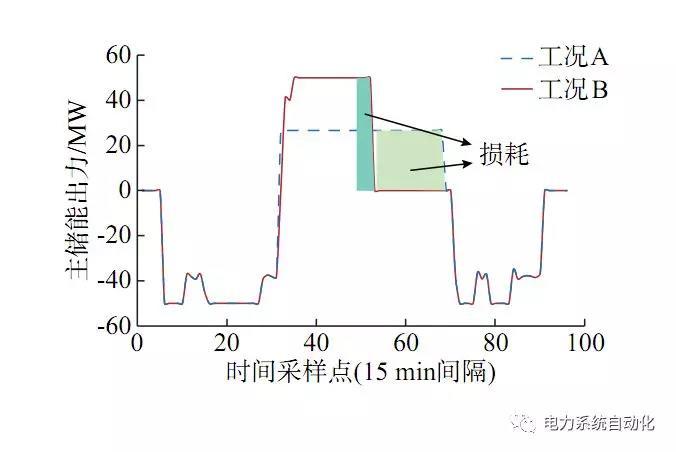
图3  两种极限工况下的储能功率曲线

2）充电时段

在充电时段，风电功率一部分直接上网发电，一部分用于储能设备充电（对应产生部分损耗）。常数效率模型下，由于不同功率对应的充电效率一样，则风电场以限值功率上网发电，风电最大出力与上网限值的差即为充电功率，这种差值方式消纳效果最佳。而在动态效率模型下，上网发电功率和充电功率之间则存在一个优化问题。图4给出了动态效率下充放电全时段优化后的主储能出力曲线，比B工况增加12.88MW·h，相对提升6.0%，原因在于，常数效率模型下主储能的功率对效率不敏感，会出现一些时段在低效率状态运行，而动态效率模型下将会尽量避免这种低效率情况。

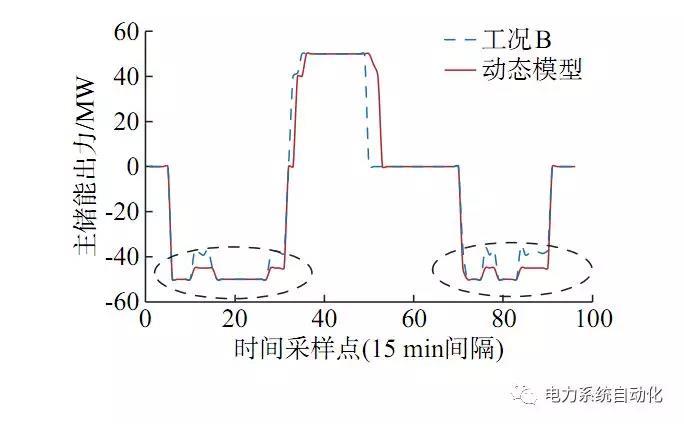
图4  两种效率模型下主储能功率曲线

4.2  混合储能对消纳效果的影响

混合储能模式下，动态效率模型优化消纳结果为245.52MW·h，对比B工况消纳结果差值为31.1MW·h，这部分的提升来自于两部分。第一部分是辅助储能在局部充放电吸收弃风，增加消纳量为15.26MW·h，增加7.12%，这部分辅助储能带来的收益对于常数效率模型下混合储能也同样存在；第二部分，采用动态效率模型带来的综合效率提升增加消纳，具体增加量为15.84MW·h，提升7.39%，这部分因素在常数效率模型中不存在。可见，小容量辅助储能的加入，在主储能低功率运行时辅助充放电，混合储能的低功率区段综合效率得以提升。

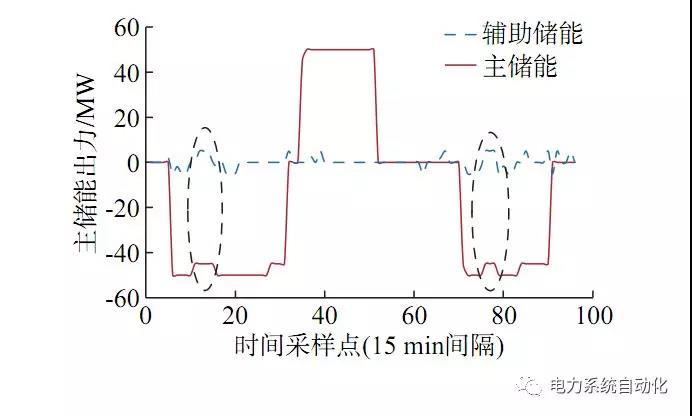
图5  动态效率模型下主储能和辅助储能功率曲线

4.3  消纳效果影响的因素分析

1）主储能容量影响分析

假设主储能的容量在170MW·h~400MW·h之间变化，得到单一储能模式下消纳提升效果与储能容量的关系曲线如图6所示（放电时段均为最大效率）。可以发现，消纳提升效果的百分比总趋势随容量增加而增加；当容量增加到一定水平后，改善效果趋于饱和，不再增加。通过这组曲线，也可以为风储联合系统的储能优化配置提供借鉴。

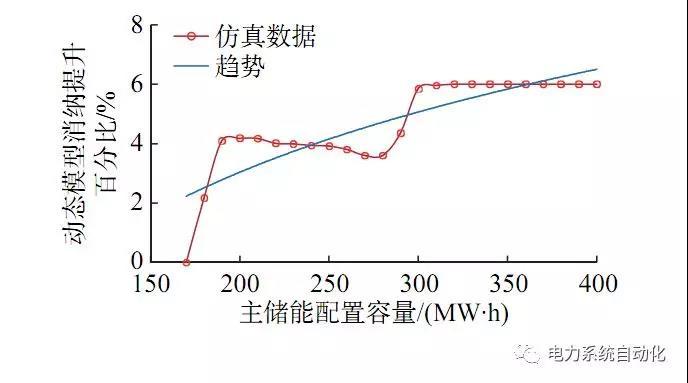
图6  消纳提升效果与储能容量的关系

2）混合储能模式下配比影响分析

图7表示了充电环节提升效果受辅助储能容量的影响，其纵坐标表示混合储能通过提高效率带来的消纳提升，这部分提升在常数效率模型中无法获得。3条曲线对应不同放电时长的辅助储能，即最大存储电量容量不同。可以看到辅助储能加入后，对动态效率的提升存在一个饱和值，这是因为当混合储能联合运行将储能都优化到高效率点以后，来自于动态效率模型的消纳提升则饱和。

图

7  消纳提升效果与辅助储能容量的关系

3）预测误差影响分析

以预测曲线计算出动态效率模型和常数模型下的出力，在预测曲线上添加随机误差（本次分析重复50次），分析两种模型下的日前优化出力在添加误差后的实际效果，其中基准值为添加误差后新曲线的最优理想消纳效果。由图8可以看到，动态模型给出的出力计划与理想最优效果差距平均为8.49%，而以B工况的出力效果与理想最优的差距平均为20.70%，在预测误差的干扰下，动态模型消纳效果受到的影响相对较小，这是动态模型下的储能出力在较高的效率区域的缘故。

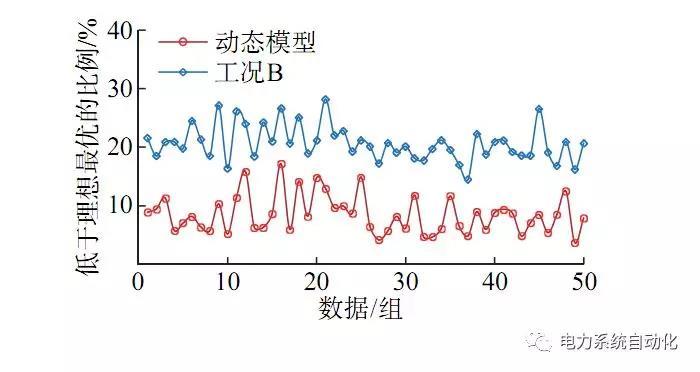
图8  预测误差对两种模型出力效果的影响

5、结论

本文以压缩空气储能和电化学储能为例，建立了储能的动态效率特性模型，在此基础上建立了混合储能-风电联合运行的混合整数优化模型，用于分析实现最大风电消纳的优化运行方式。结合理论与算例分析，发现风储联合系统中，不论充电时段还是放电时段，努力使储能工作在满足约束条件下的最大功率模式，可有效提升风电消纳效果，采用动态效率模型能够更精确刻画其储能效率。主储能容量和混合储能配比影响消纳效果，随着主储能容量增加，动态效率模型的消纳提升效果越显著，但这种增效存在饱和特性；在此基础上，辅助储能能带来额外提升，但同样存在饱和现象。

与常数模型优化运行相比，动态效率模型受误差随机性的影响有所减少，但仍然存在。本文对效率模型受误差影响的研究尚有局限，预测误差对动态效率影响的量化及依此进行储能出力的修正将是进一步的研究方向。