中国储能网讯:
摘 要 为了研究传送链式斜坡重力储能系统(transmission chain slope gravity energy storage system,TCS-GESS)充放电过程的能量转换效率及各环节损耗占比,针对系统质量块移动、机械传动以及电气驱动环节,推导了各环节损耗数学表达式及相应的能效计算方法,在此基础上,建立了基于MATLAB/Simulink的TCS-GESS能效分析模型。以一套2.2 kW重力储能样机为例,设计了充放电工况下的实验方案并实测了不同负载条件下系统各环节能效,从速度、机械功率、充放电功率、传动损耗以及电机损耗五个维度与能效计算结果进行对比,验证了能效分析模型的准确性与实用性。结果显示,随负载增加系统效率逐渐提高,其中链条损耗占比较大,齿轮箱和齿轮盘损耗变化不大且占比较小,电机损耗占比中等且充/放电工况下随着加载均有所增加。额定负载工况下充放电效率分别为59.5%和37.4%,系统效率为23.2%;进一步对具有相同传动机构、不同功率等级下重力储能系统充放电效率进行预测,结果表明系统容量低于1 MW时充放电效率将低于68%,容量高于10 MW时系统能效提升潜力有限,即采用文中传动机构的重力储能单机系统最佳功率范围宜选取在1~10 MW。
关键词 重力储能系统(GESS);链式传动;损耗计算;能效模型
储能技术在平滑间歇式能源功率波动、削峰填谷以及提供灵活功率调节等方面发挥了巨大的作用,重力储能作为一种新兴物理储能技术备受关注。目前,重力储能系统在结构上主要分为垂直式与斜坡式两种。对于垂直式重力储能系统,Energy Vault(EV)公司提出了一种塔吊式重力储能技术,并在瑞士提契诺州建设了5 MW/35 MWh的示范工程。Gravitricity公司提出了矿井式重力储能技术,可实现废弃矿井再利用并实现储能。文献[7]提出了一种活塞式重力储能系统,相比于其他形式的重力储能系统具有较高的安全性能。中国天楹公司引进了EVx技术方案,建设了全球首个百兆瓦时示范工程——江苏如东25 MW/100 MWh储能项目,该工程于2023年9月封顶,并于2024年5月完成首套充放电单元测试。对于斜坡式重力储能系统,Advanced Rail Energy Storage(ARES)公司提出的轨道机车储能结构,其效率高达80%,且系统寿命达40年以上。天津大学提出利用斜坡轨道和码垛机进行重力势能储能的构想。文献[10]提出了两种重载车辆爬坡储能方案。
除了上述对重力储能系统本体结构设计的研究外,在系统本体的控制策略及外特性方面,文献[11]从质量块码放环节分析,优化控制方法,改善了质量块码放时效性;文献[12]提出了可用于快速响应负荷需求的两段式斜坡重力储能系统,实现对放电功率的快速调节;文献[13]提出了重力储能电站机组容量配置策略及其控制方法实现了储能效率和稳定性的优化。此外,还有学者针对斜坡轨道式重力储能系统本体开展了研究,比如文献[14]分析了系统全过程能量损耗情况,研究了不同因素对系统效率的影响情况;文献[15]分析了重力储能系统效率关键影响因素,并与风电场耦合调度结合,提高风电利用率。上述文献对斜坡式重力储能影响因素的研究仅从斜坡角度、运行速度、质量块质量三个维度分析,缺乏各结构组成部件在不同运行工况下对系统运行效率影响分析,同时斜坡重力储能系统在传动机构方面存在多种类型选择,传送链式斜坡重力储能系统(transmission chain slope gravity energy storage system,TCS-GESS)作为典型的系统方案,还未有学者对其进行完整的能效分析。
针对上述问题,为研究传送链式斜坡重力储能系统充放电过程的能量转换效率及各环节损耗占比,本工作针对系统质量块移动、机械传动以及电气环节,推导了各环节损耗数学表达式及相应的能效计算方法,建立了基于MATLAB/Simulink的TCS-GESS能效分析模型,仿真结果与实测能效数据基本一致,验证了能效分析模型的准确性与实用性,实现了TCS-GESS各环节的损耗占比分析,同时预测具有相同传动机构、不同功率等级下重力储能系统的充放电效率,得到了采用相同传动机构重力储能单机系统的最佳功率范围。
1 传送链式斜坡重力储能系统
1.1 结构组成及功能
传送链式斜坡重力储能系统主要由质量块承载车(包含质量块)、链条、齿轮盘、齿轮箱以及电机五个部分组成(图1)。质量块(放置于承载车中)作为固体储能介质,是电能与重力势能相互转换的媒介。链条与质量块承载车相互衔接,起到传动作用;包围链条的支撑轨道起动支撑作用;齿轮盘与链条相互衔接,起动力传输作用;齿轮箱利用主从轮的齿数差,起改变输出转速及转矩的作用;电机作为电动/发电设备,系统充电时为质量块提供动力,系统放电时质量块重力势能转化为电能回馈至电网。
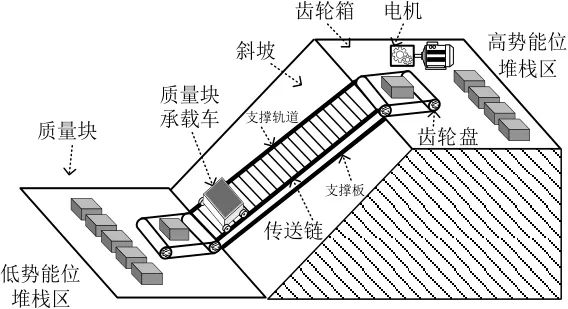
图1 传送链式斜坡重力储能系统
1.2 工作原理
重力储能系统运行分为充放电两种工况,其能量转化过程如图2所示。充电工况下,重力储能系统从新能源侧获取电能,电机工作于电动工况,转子旋转带动质量块从低势能位向高势能位移动,电能转化为重力势能。放电工况下,质量块从高势能位释放,向低势能位移动,反拖电机转子发电,重力势能转化为电能回馈至电网。
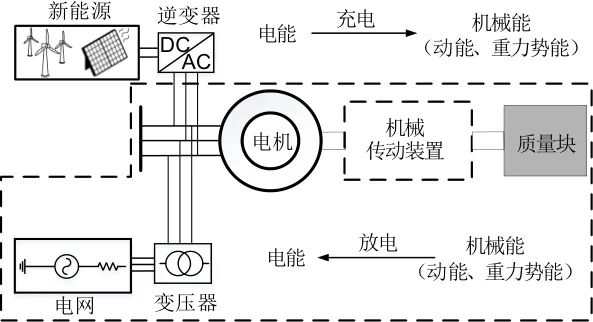
图2 能量转换过程
1.3 重力储能损耗分析
重力储能系统损耗环节包括机械环节、电气环节、搬运环节以及堆栈环节。根据图1所示结构,质量块在上行或下行过程中,放置于质量块承载车中和传送链相互衔接同步运行,期间质量块承载车与支撑轨道、传送链各链节、传送链与支撑板、传送链与齿轮盘、齿轮箱及电机均会产生摩擦损耗(图3),同时由于工况不稳定而引起的不可控损耗具有随机变化、占比较小的特点,故本工作将其忽略。
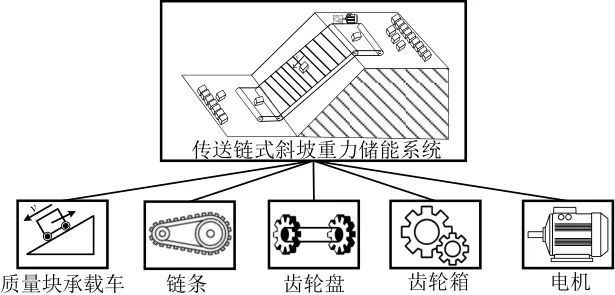
图3 系统结构部件损耗解析
对于传送链式斜坡重力储能系统,质量块承载车在沿斜坡上行(充电)或下行(放电)过程中为直线运动,损耗以摩擦力形式呈现,而齿轮盘、齿轮箱及电机等部件工作时为旋转运动,损耗以摩擦转矩形式体现,为统一分析重力储能系统损耗,将各环节损耗转化并折算到电机轴端以转矩形式进行计算。
2 重力储能系统损耗计算方法
鉴于堆栈环节与搬运环节的损耗随系统结构、系统容量、码放方式、搬运路径等多种因素的不确定性,故仅考虑重力储能系统质量块上下运行过程中的损耗,暂不考虑堆栈环节以及搬运环节引起的损耗。
2.1 质量块承载车
在质量块承载车(包含质量块)沿着斜坡运行的过程中,承载车与支撑轨道,两者之间相互摩擦,阻碍质量块上行或下行,产生摩擦损耗[16]。将上述摩擦损耗折算至电机轴端,如式(1)所示。
式中,Tf为质量块承载车摩擦损耗折算至电机轴端;Pf为质量块承载车所产生摩擦损耗;μ为斜坡摩擦系数;m为质量块承载车(包含质量块)质量;v为承载车的运行速度;θ为斜坡角度;rgp为齿轮盘半径;i为齿轮箱变比。
2.2 链条
链条分为上下两部分,即紧边与松边。在承载车与链条同步运行时,紧边各链节间受力导致相互挤压产生损耗,松边与底部支撑板产生损耗[17]。将上述损耗折算至电机轴端如式(2)所示。
式中,Fc1为链节间摩擦力;Fc2为松边与底部支撑板间摩擦力;μ1为链节摩擦系数;μ2为松边与垫片摩擦系数;Tc为链条摩擦损耗折算至电机轴端;Pc为链条所产生摩擦损耗。
2.3 齿轮盘
在链条运行过程中,链节与齿轮盘相互啮合产生摩擦损耗[17]。将上述摩擦损耗折算至电机轴端,如式(3)所示。
式中,Tgp为齿轮盘损耗折算至电机轴端;μ3为齿轮盘摩擦系数;m1为齿轮盘自重;rgp为齿轮盘半径;N为齿轮盘转速;Pgp为齿轮盘损耗。
2.4 齿轮箱
齿轮箱损耗主要包括滚动损耗、摩擦损耗、搅油损耗、风阻以及轴承损耗[18-19]。
当齿轮传动系统运转时,齿轮之间会发生滚动,齿轮啮合处由于齿轮齿面间的接触和滚动而产生摩擦,造成滚动损耗,如式(4)所示。
式中,Pgrf为齿轮箱滚动损耗;k为比例系数;h为油膜厚度;α为端面压力角;β为基圆压力角;Lgb为啮合线长度;z1为主动轮齿数;z2为从动轮齿数。
当齿轮传动系统运转时,齿轮的啮合不可能完全理想,会导致一定程度的齿轮齿面之间的滑动,此时会产生摩擦损耗,如式(5)所示。
式中,Pgsf为齿轮箱的滑动损耗;k1为比例系数。
齿轮箱齿轮运转会引起油液的搅动和摩擦,这会导致油液温度升高和部分油液被气泡化,从而降低了润滑效果,并产生了搅油损耗,如式(6)所示。
式中,Pocl为齿轮箱的搅油损耗;k2为比例系数;fg为齿轮浸油系数;N1为电机轴转速;ν0为润滑油黏度;D为齿轮在润滑油内的直径;b为齿宽;Ag为齿轮列数;Rf为齿面粗糙度;B为螺旋角角度。
周围空气会对齿轮箱表面施加压力,形成风阻,阻碍设备正常运行,该部分损耗如式(7)所示。
式中,PW为齿轮箱的风阻;k3为比例系数;r1为主动轮分度圆半径。
齿轮箱中的轴承在支撑和引导齿轮旋转时,相互摩擦产生轴承损耗,如式(8)所示。
式中,Pbl为齿轮箱的轴承损耗;Tbl为传递到齿轮箱轴承的力矩;f0为轴承浸油因数;f1为轴承载荷及结构相关系数;dm为轴承中径。
将齿轮箱损耗折算至电机轴端如式(9)所示。
式中,Tgp为齿轮箱损耗折算至电机轴端;ωgb为齿轮箱输出轴角速度。
2.5 电机损耗
电机中的损耗主要包括铜损、铁损、机械损耗和杂散损耗四种类型,分别体现在电气和机械两部分。
2.5.1 电气部分
电流通过电机绕组时在导线电阻上产生电机铜耗,电机铁心中的交变磁场引起电机铁耗,电机绕组中因谐波漏磁磁场引起杂散损耗,三者即为电机电气损耗[20],如式(10)所示。
式中,Pel为电机电气损耗;PN为电机的额定功率;∆PN为额定损耗;∆PW为不变损耗;η为额定效率;PFe和Pwind分别为电机的铁心损耗和风摩耗;β为电机的负载率。
2.5.2 机械部分
电机机械损耗包括转子与空气产生的摩擦损耗(风摩耗)以及转子与轴承之间的摩擦损耗(轴承损耗),如式(11)所示。
式中,krc为转子表面粗糙度系数,转子表面光滑为1;ρair为空气密度;rrotor为转子半径;Cf为空气摩擦系数;lef为转子轴向长度;Tmotor为轴承摩擦损耗折算至电机轴端;Pmotor为轴承摩擦损耗;Bg为轴承摩擦系数。
3 实验与仿真
3.1 TCS-GESS能效分析模型
依据上文各环节损耗数学表达式及相应的能效计算方法,建立基于MATLAB/Simulink的TCS-GESS能效分析模型。首先,能效分析包括质量块模型和传动环节模型,与损耗计算模块结合,可实现各环节损耗占比分析。其次,通过等效输入转矩计算模块得到实际工况下的负载转矩,将其输入至电机模块,实现重力储能系统的工况模拟。最后,速度转换模块将电机轴端的角速度转化成电机轴转速与质量块运行速度,反馈于各环节模型,实现动态闭环响应,如图4所示,其中T1为质量块等效转矩,T2为经传动环节后输入至齿轮箱的转矩,Tm为电机轴端转矩,P2为经传动机构后的损耗功率,Ptotal为系统功率损耗的总和。
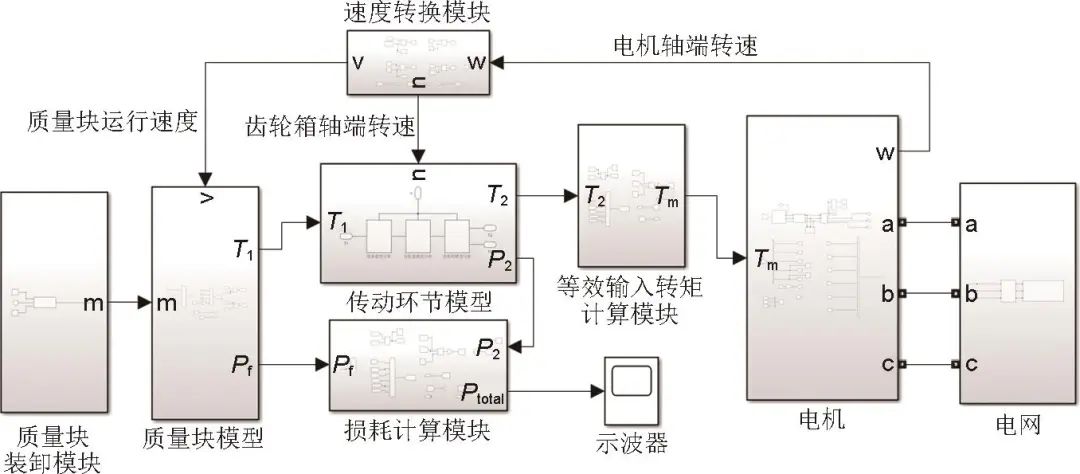
图4 传送链式斜坡重力储能系统能效分析模型
3.2 实验方案设计
为验证能效分析模型的可行性,以图5所示的一套2.2 kW重力储能样机为例,设计了充放电工况下的重力储能系统实验方案。其中,电机采用2.2 kW异步电机,斜坡长为7.6 m,角度为34.6°。实验过程中采用由轻载逐渐升为满载状态的方式,对应质量块质量分别为198.65 kg、255.8 kg、314.65 kg、358.9 kg以及403.15 kg。为方便操作,实验采用沙袋作为质量块。

图5 重力储能系统实验装置
实验中,通过测量稳态下的齿轮箱转速,计算变比,得到质量块实际运行速度。采用功率分析仪测量电机侧输出放电功率、输出电流及输出电压情况,并依此计算电机损耗和传动损耗。其中,由于实验中电机轴承损耗无法实测,故将这部分损耗归于传动损耗部分。充电工况下系统各环节功率满足式(12),放电工况下系统各环节功率满足式(13)。
式中,PG为电动/放电功率;Pmass为质量块机械功率;Ploss为传动损耗;Pmotor为电机损耗。
3.3 仿真与实验对比
3.3.1 速度
图6为充放电工况下质量块加载变化时质量块稳态运行速度响应特性。由于实验样机采用异步电机,根据其运行特性可知,在不同负载条件下,由于负载(机械)转矩与电磁转矩的平衡点不同,稳态时刻电机转速会发生规律性变化。
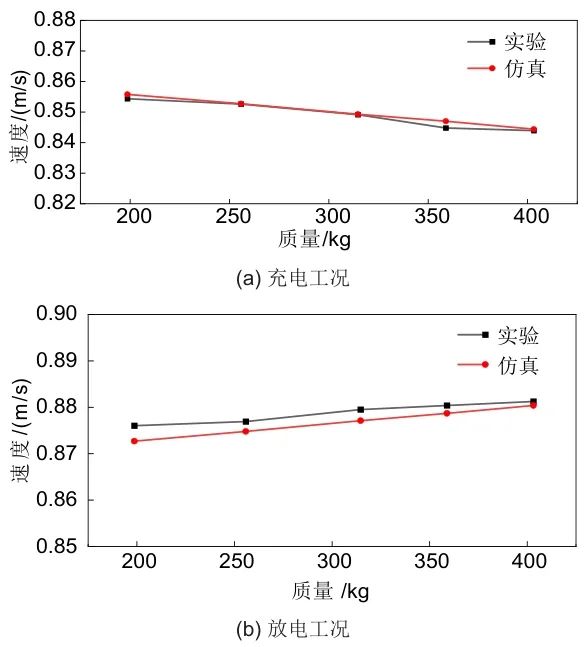
图6 质量块稳态运行速度响应特性
充电工况下,实际转速低于同步转速,随着负载转矩的增加,为了提供更多的电磁转矩,转差率增加导致稳态转速下降,从而保持负载与转矩平衡;放电工况下,实际转速高于同步转速,转差率为负值,随着机械转矩的增加,转差率减小,幅值增加,转速上升以产生足够的反作用转矩来平衡增加的机械转矩,并维持稳定的放电状态。
3.3.2 机械功率
图7为充放电工况下质量块加载变化时质量块输出机械功率响应特性。由P=mgvsinθ可知,机械功率输入/输出与斜坡角度、质量块质量及其运行速度呈正相关,其中本实验样机系统采用的斜坡角度为固定值。
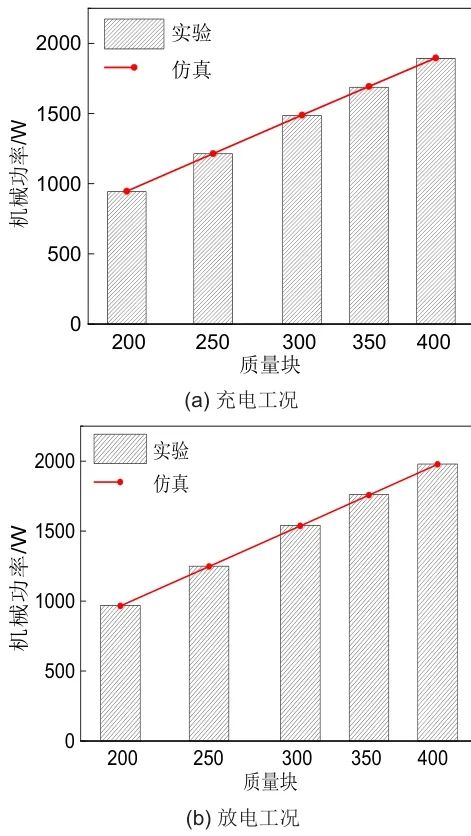
图7 质量块机械功率响应特性
充电工况下,负载增加时,对应于质量块质量增加,速度微弱减少,前者变化数量级远大于后者,故整体呈现增大趋势,如质量由314.65 kg增加至358.9 kg时,运行速度由0.84913 m/s减少至0.84479 m/s,质量变化功率增幅为209.31 W,速度变化功率衰减为7.61 W,故此过程中机械功率输出增加;放电工况下,负载增加时,对应于质量块质量增加,速度微弱增加,故整体呈现增大趋势。
3.3.3 充电/放电功率
图8为充放电工况下质量块加载变化时电机充/放电功率响应特性。
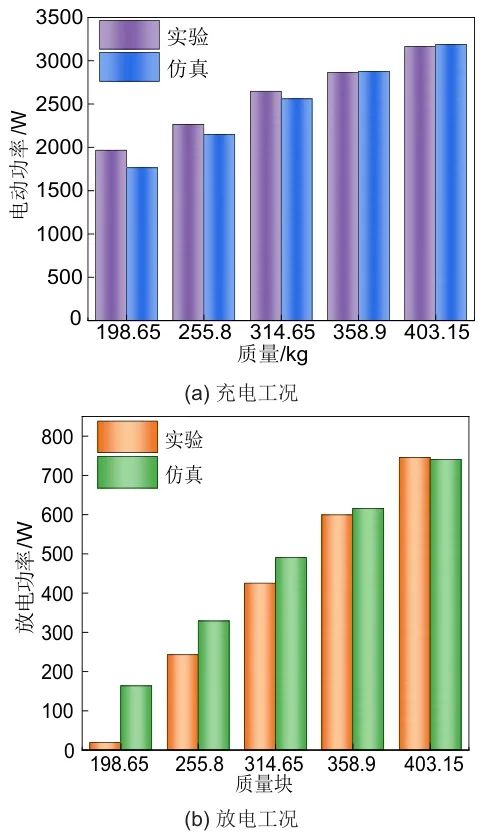
图8 充放电功率响应特性
充电工况下,异步电机电功率以电动功率形式体现,在数值上为机械功率与各类损耗功率之和,负载增加时,两者均增加,故整体呈增大趋势;放电工况下,异步电机电功率以放电功率形式体现,在数值上为机械功率与各类损耗功率之差,负载增加时,前者增幅远大于后者,故整体现增大趋势,如质量由314.65 kg增加至358.9 kg时,机械功率增幅为218.534 W,各类损耗功率增幅为40 W,故此过程放电功率增加。
3.3.4 传动损耗及电机损耗
图9与图10分别为充放电工况下质量块加载变化时传动损耗和电机损耗响应特性。
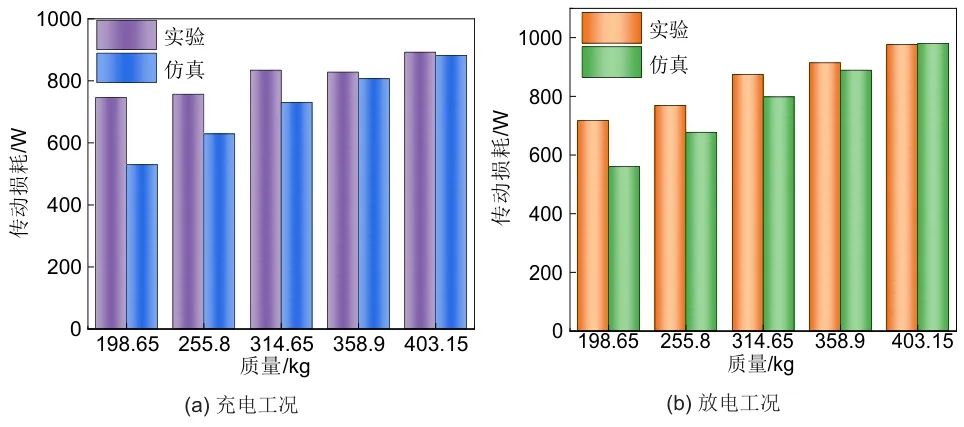
图9 传动损耗响应特性

图10 电机损耗响应特性
此处传动损耗为系统中任何传动环节所造成的损耗之和,包括了质量块承载车与支撑轨道、传送链各链节、传送链与支撑板、传送链与齿轮盘、齿轮箱及轴承之间的损耗;由式(1)和式(2)可得,前三者与质量块质量及其运行速度呈正相关,随负载增加而增加;由式(3)、式(9)及式(11)可得,后三者与电机转速、扭矩呈正相关,随负载增加而增加;故当负载增加时,传动损耗整体呈增大趋势。电机损耗包括可变损耗和不可变损耗两部分,由式(10)可得,可变损耗随负载增加而增加。
3.3.5 充电/放电效率
图11为充放电工况下质量块加载变化时系统充/放电效率响应特性。电动效率为质量块机械功率与上述电动功率之比,随着负载增加,两者均增加,但各类损耗功率增幅不大,使两者增幅差异不大,故整体呈现增大趋势,如质量由314.65 kg增加至358.9 kg时,机械功率由1486.81 W升至1687.23 W,增幅为200.42 W,电动功率由2647.81 W升至2866.63 W,增幅为218.82 W,故此过程中放电效率增加;放电效率为上述放电功率与质量块机械功率之比,随着负载的增加,两者均增加,但各类损耗功率增幅不大,使两者增幅差异不大,故整体呈现增大趋势,如质量由314.65 kg增加至358.9 kg时,机械功率由1541.59 W升至1760.13 W,增幅为218.54 W,放电功率由425.39 W升至599.33 W,增幅为173.94 W,故此过程中放电效率增加。
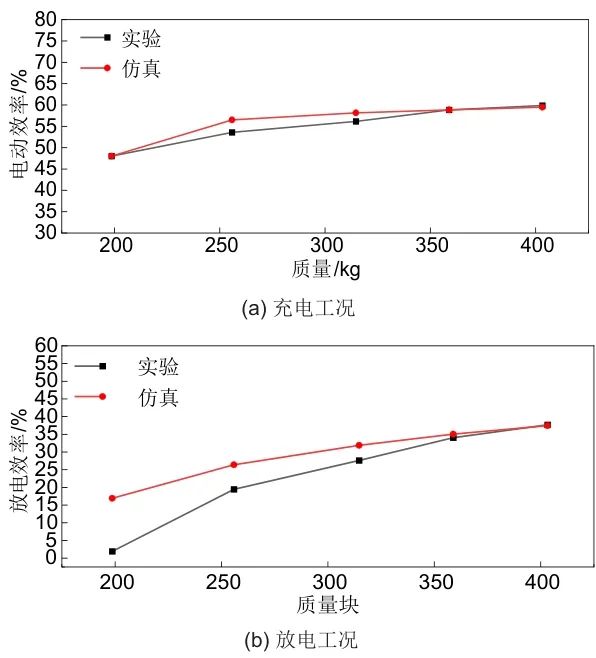
图11 系统充放电效率响应特性
3.3.6 系统总效率
图12为充放电工况下质量块加载变化时系统总效率响应特性。系统总效率为上述放电功率与上述电动功率之比,其中传动损耗与电机损耗在低负载时占比例较大,而在高负载时占比减少,故当负载增加时,系统总效率呈增大趋势。
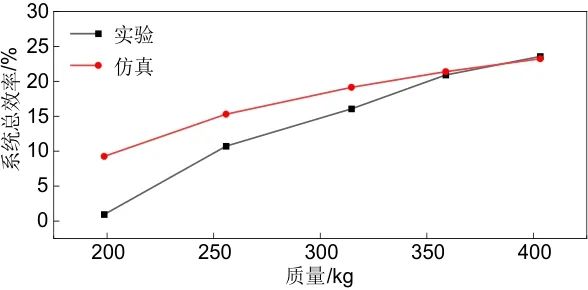
图12 系统总效率响应特性
结果表明,轻载时受实验环境及质量块无法正常出力影响,系统样机阻力较大,不可控损耗以电机损失电功率的形式承担,工况波动造成传动损耗较仿真有所增加,故导致实验与仿真存在差异;在额定负载工况下,不可损耗占比变小且工况逐渐稳定,从上述五个维度仿真结果与实测能效数据基本一致,且变化规律与前述理论吻合,验证了能效分析模型的准确性与实用性。
3.4 系统损耗占比分析
基于上述能效分析对传送链式斜坡重力储能系统各模块损耗进行分析,质量块承载车与支撑轨道、传送链各链节、传送链与支撑板之间的损耗与质量块质量及其运行速度呈线性正相关,随负载增加而增加,且增幅较大;齿轮盘、齿轮箱及轴承间损耗与电机转速、扭矩呈正相关,随负载增加而增加,实际运行中速度变化微弱,故增幅不大。电机损耗则与负载率相关,随负载增加而增加,占比与系统容量相关。
3.4.1 充电工况
在不同负载条件下,基于能效分析模型进一步分析可得充电工况下各损耗模块占比情况,见表1,其中图13为额定充电工况下各损耗占比。结果表明,在整个系统损耗中链条运行损耗占比较大,且随着逐渐加载的过程中,损耗增幅较大。与转速直接相关的齿轮箱和齿轮盘损耗变化不大且占比较小。电机损耗占比中等,且随负载增加而增加,变化规律与前述理论分析吻合。随着质量块不断加载,系统充电效率逐渐提高,额定工况下可达59.5%。
表1 不同负载下充电工况各损耗占比

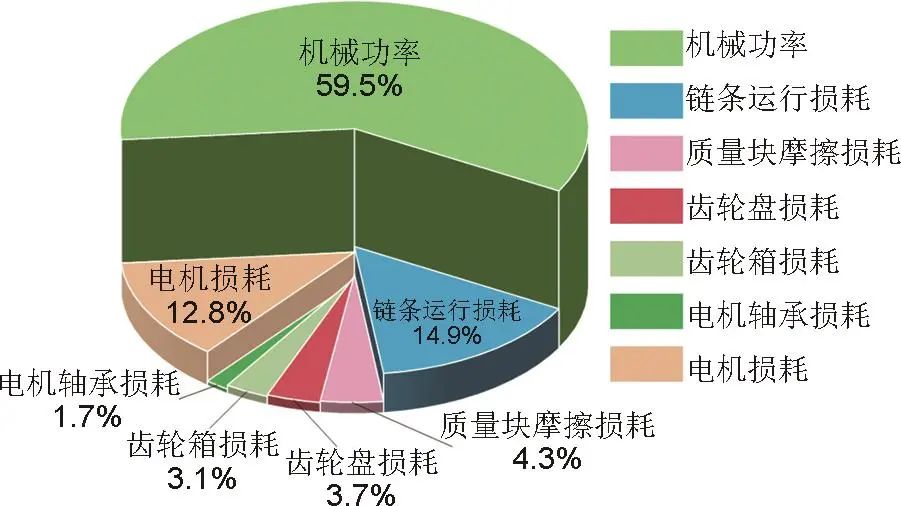
图13 额定充电工况下各损耗占比
3.4.2 放电工况
在不同负载条件下,基于能效分析模型展开进一步分析,得放电工况下各损耗模块占比情况,见表2,其中图14为额定工况下各损耗百分比占比。结果表明,在整个系统损耗中链条运行损耗占比较大,且随着逐渐加载的过程中,损耗增幅较大。与转速直接相关的齿轮箱和齿轮盘损耗变化不大且占比较小。电机损耗占比中等,随动力增加而增加,变化规律与前述理论分析吻合。随着质量块不断加载,系统放电效率逐渐提高,额定工况下可达37.4%。
表2 不同负载下放电工况各损耗占比

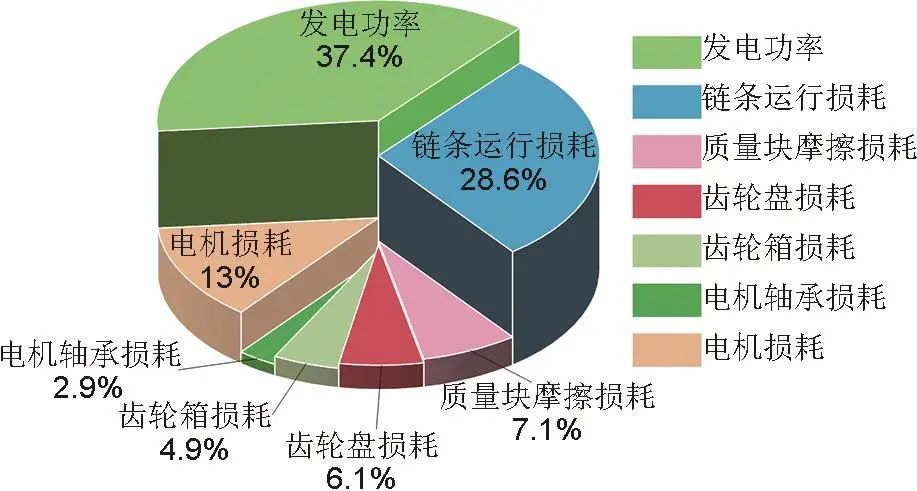
图14 额定放电工况下各损耗占比
3.5 不同功率等级下系统的效率预测
采用小容量系统样机能效分析的结果作为理论基础,对大容量系统样机效率进行预测分析:对于具有相同传动机构的重力储能系统,在质量块运行速度及电机转速相同的情况下,齿轮盘与齿轮箱损耗基本不变,质量块承载车与支撑轨道、传送链各链节、传送链和支撑板部分损耗与负载呈线性变化,故当系统容量提升时,相比于小容量样机,初始增加阶段,齿轮盘等损耗占比不小,起到影响效率提升的负效应,但电功率增幅更大,故效率整体呈现增大趋势;随着容量进一步增加,线性变化的损耗作为主导因素,使电动功率与放电功率增幅规律一致,故增加至一定程度时会使效率变化趋势变缓;若进一步增加容量,效率增益较小且会带来较大的成本消耗。
利用本模型对具有相同传动机构、不同功率等级下的重力储能系统充放电效率进行预测,分别以100 kW、1 MW、5 MW、10 MW、100 MW为例。充放电功率均对应同等质量下的质量块进行仿真,结果见表3。可以看出,效率随着重力储能系统功率等级的提升而增加,但是当功率等级进一步提升时,系统效率增益较弱,故通过仿真结果得到的变化规律与前述理论分析吻合。
表3 不同功率等级下重力储能系统充放电效率预测
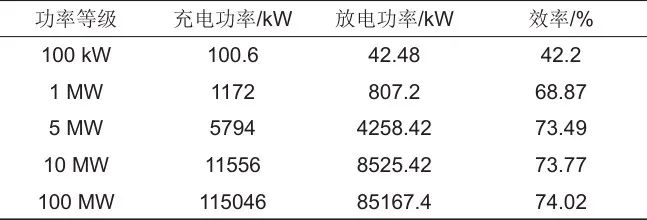
结果表明,当系统容量低于1 MW时充放电效率将低于68%,容量高于10 MW时系统能效提升潜力有限,即采用文中传动机构的重力储能单机系统最佳功率范围宜选取在1~10 MW。
4 结论
从TCS-GESS质量块承载车损耗、链条损耗、齿轮盘损耗、齿轮箱损耗以及电机损耗等五部分研究了其充放电过程的能量转换效率及各环节损耗占比,所得结论如下:
(1)推导了各环节损耗数学表达式及相应的能效计算方法,建立了基于MATLAB/Simulink的TCS-GESS能效分析模型。并设计了充放电工况下的TCS-GESS实验方案,利用能效分析模型从速度、机械功率、充电/放电功率、传动损耗以及电机损耗五个维度进行仿真,仿真结果与实测能效数据基本一致,验证了能效分析模型的准确性与实用性。
(2)系统效率随负载增加逐渐提高,其中链条损耗占比较大,齿轮箱和齿轮盘损耗变化不大且占比较小,电机损耗占比中等且充/放电工况下随着加载均有所增加;额定负载工况下充放电效率分别为59.5%和37.4%,系统效率为23.2%。
(3)进一步对具有相同传动机构、不同功率等级下重力储能系统充放电效率进行预测,结果表明系统容量低于1 MW时充放电效率将低于68%,容量高于10 MW时系统能效提升潜力有限,即采用文中传动机构的重力储能单机系统最佳功率范围宜选取在1~10 MW。





