中国储能网讯：

摘 要 透平膨胀机是二氧化碳储能系统的关键装备，透平叶轮的结构参数优化有利于更好地提高透平膨胀机的整体性能。本文以某百千瓦级二氧化碳储能系统向心透平为研究对象，首先通过气动设计得到该二氧化碳透平的主要结构参数，然后基于Numeca开展流场仿真，分析了叶轮叶片数、叶轮入口角和叶轮出口角对流动特性的影响规律，进一步研究了叶顶间隙内的泄漏流和损失，最后探究了非定常流动特性下透平性能的变化规律。结果表明：随着叶轮叶片数的增加，叶轮流道中的低马赫数区域占比先降低后增加；叶轮入口角和叶轮出口角显著影响透平内流动分离区域和涡面积分布，优化叶轮角后的透平等熵效率达83.65%，较初始设计提高了0.75%；透平等熵效率随叶顶间隙的增加而减小，且近似呈线性变化；喷嘴尾迹流会引起叶轮内的非定常流动，且透平等熵效率较定常工况时下降了0.57%。

关键词 二氧化碳储能；透平膨胀机；结构参数；叶顶间隙泄漏；非定常流动

为应对化石能源可持续利用和温室气体排放带来的能源和气候问题，发展可再生能源已成为国内外的广泛共识。然而，风电、光伏等可再生能源具有显著的波动性和间歇性，大规模可再生能源电力并网会影响电网的稳定运行，而储能技术被视为应对该问题的有效措施之一。二氧化碳储能是一种新型压缩气体储能技术，可有效解决大规模长时储能的地理性依赖，且具有运行寿命长、储能效率高、储能密度大等技术优势，因此受到国内外学者的广泛关注。

在二氧化碳储能系统优化设计方面，Wang等提出了一种液态存储型二氧化碳储能系统，通过参数化分析表明系统的往返效率可以达到56.64%。Liu等对比了采用两个地下储气室的跨临界和超临界二氧化碳储能系统，结果表明超临界系统的结构布局更简单，跨临界系统的往返效率和㶲效率更高，分别为63.35%和53.02%。Li等将二氧化碳储能系统与二氧化碳热泵系统相结合，以提高数据中心能效，在储能的同时实现制冷和生活供热。Liu等对跨临界二氧化碳储能系统进行了热力学和先进㶲分析，发现相比于压缩机效率，膨胀机效率对于系统性能的影响更为显著。

从设备与系统关系上看，膨胀机是二氧化碳储能系统的主要组成部件之一，直接影响系统稳定持续放电，对系统储能效率具有重要影响。从透平形式区分，速度型膨胀机主要包括向心透平膨胀机和轴流透平膨胀机。向心透平的单级膨胀比更高，且重量较轻，适用于小流量工况。Zhou等设计了1.5 MW超临界二氧化碳(SCO2)向心透平，在设计工况下，一维结果与模拟结果基本吻合，透平内无明显的流动分离区域，在非设计工况下，两者的相对偏差在5%以内。Lv等对SCO2透平的损失关系式进行了筛选验证，并利用序列二次规划算法对设计参数进行优化，优化后透平在大部分工况下性能得到提升。Uusitalo等分析了功率尺度和比转速对SCO2向心透平设计和性能的影响，在0.1～3.5 MW范围内，最佳比转速范围为0.5～0.6。随着比转速的增加，静叶损失所占份额减小，而叶顶间隙和出口动能损失所占份额增加。Zhou等对SCO2布雷顿循环进行了参数优化，并对向心透平进行设计分析，透平在设计工况和非设计工况下均能保持较好的性能。施东波等提出了基于Gauss过程回归的一维优化设计方法，优化后透平效率由83.68%提高至91.20%。

文献综述表明，除叶轮热力设计和流动损失模型研究之外，鉴于透平内流体的三维流动特征，结构参数也会对透平性能产生显著影响。因此，通过结构参数优化满足设计工况下CO2向心透平的最佳性能，显得尤为重要。此外，现有CO2向心透平研究多基于超临界二氧化碳布雷顿循环，面向二氧化碳储能循环所需的大膨胀比宽负荷透平膨胀机的研究还较少。针对储能系统周期性发电和变工况特性，进一步分析CO2向心透平内的非稳态流动也是很有必要地。

综上所述，本文首先对二氧化碳储能系统向心透平进行气动设计，其次分析了叶轮叶片数、叶轮入口角、叶轮出口角和叶顶间隙对透平性能的影响，最后分析了透平非定常流动与透平整体性能的关系。

1 CO2向心透平设计及流场分析

1.1 CO2向心透平设计及建模

二氧化碳储能系统通过将热力学能、压力势能与电能进行相互转换，以此实现能量的存储与释放。作者所在团队于2023年在河北廊坊建设了百千瓦级液态二氧化碳储能示范验证系统，并就系统工艺流程优化和关键设备开发开展研究。该系统在典型工况下的理论储能效率可达55%左右，系统的总体布局如图1所示。CO2透平作为主要的做功部件，通过将高温高压的二氧化碳进行膨胀降压并带动发电机发电。该二氧化碳储能系统向心透平的主要设计参数如表1所示。

图1   百千瓦级二氧化碳储能系统 (a) 及其透平膨胀机 (b)

表1   CO2透平的设计参数

首先对CO2向心透平进行一维设计，在设计时尽量保证透平效率最大，透平效率的表达式如式(1)所示。此外需要考虑喷嘴出口马赫数、叶轮冲角、相对马赫数等的限制，选择合适的特性比和反动度，并确定喷嘴速度系数、叶轮速度系数、轮径比等参数的取值。该透平的主要设计结果如表2所示。

表2   CO2透平的主要设计结果

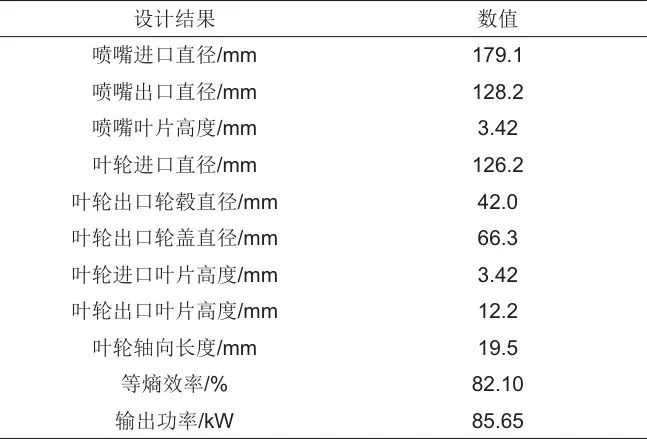
根据一维设计结果，利用涡轮机械设计软件Concepts NREC对透平进行模型构建，将生成的结构导入仿真软件Numeca中进行数值分析。在Autogird5中进行网格划分，为捕捉边界层内的流动，需要对近壁面网格进行加密，参照式(2)分别确定喷嘴和叶轮的近壁面网格宽度。

网格划分之后，需要设置边界条件和流动模型，以模拟透平内的流动情况。入口边界条件给定总温、总压和速度方向，出口边界条件给定平均静压。动静交界面采用混合平面法，考虑计算的准确性和收敛速度，采用SA湍流模型。对网格进行无关性验证，不同网格数量的模拟结果如图2所示。对于单流道的喷嘴和叶轮，当网格数量在第4组214万时，透平等熵效率和输出功率基本不发生变化。此时喷嘴和叶轮的网格结构如图3所示。

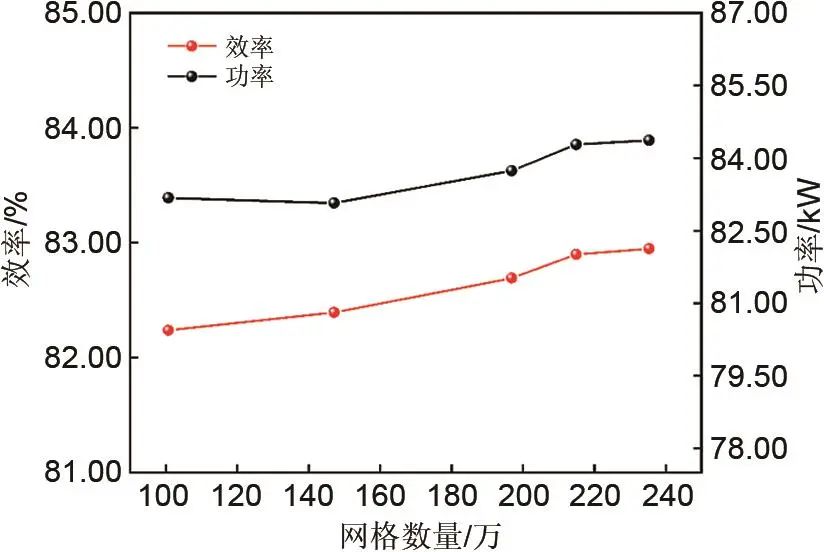
图2   网格无关性验证

图3   喷嘴和叶轮网格

1.2 CO2向心透平流场分析

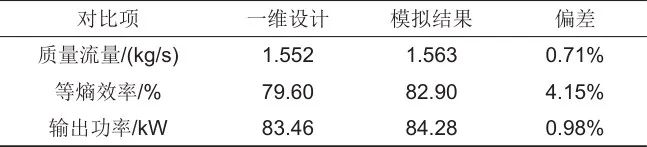
利用Numeca的Euranus求解器对CO2向心透平进行流场模拟，模拟结果与设计计算结果的对比如表3所示，设计值与模拟值的偏差小于5%，表明该设计较为合理。两者在等熵效率方面的偏差最大为4.15%，主要是因为一维设计时多采用经验关系式对透平内的损失进行估计，但透平内的流动是三维和黏性的，在流道中往往存在流动分离、回流和二次流等复杂流动，所以损失估算时存在偏差。

表3   设计结果与模拟结果对比

在设计工况下，透平内的流场分布如图4所示。透平内的流线分布较连续，无明显的速度突变，沿着整个流道，CO2绝对速度逐渐降低。叶轮出口相对速度大于入口相对速度，以确保不会产生回流。透平局部有涡存在，在喷嘴尾缘和叶轮吸力面轮盖处存在漩涡，喷嘴尾缘涡的产生是由喷嘴吸力面和压力面流体的汇聚引起的，叶轮吸力面轮盖处的涡是由叶顶间隙处的泄漏流引起的。叶顶间隙处的泄漏流如图5所示，压力面的部分流体由叶顶间隙泄漏到吸力面，形成二次流动，进而影响主流流场并减小做功量。

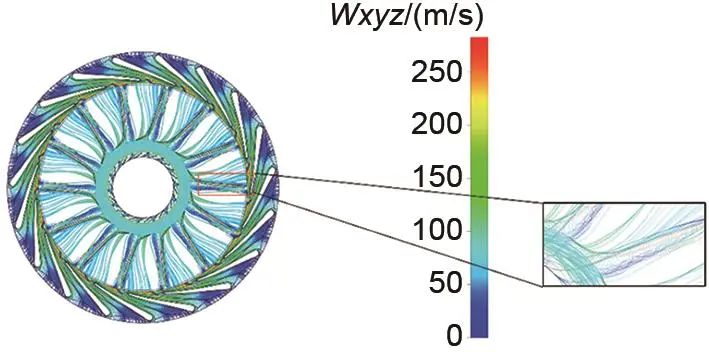
图4   透平内的流场分布

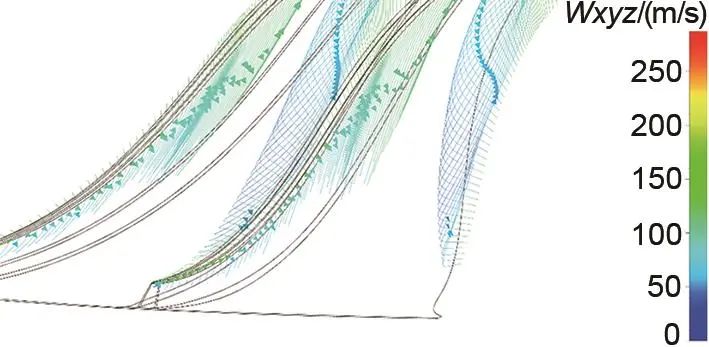
图5   叶顶间隙泄漏流

该CO2透平内的静压、静温分布如图6所示。CO2首先进入喷嘴流道，在喷嘴中温度变化较快，由于叶片厚度的影响，喷嘴叶片尾缘处会产生高温尾迹。之后工质流入叶轮流道，叶轮内的温度变化主要集中在后半部分，由于泄漏流动的影响，叶轮轮盖处会出现低温区域。CO2透平内压力的变化较为均匀，在叶轮叶片尾缘，由于压力面与吸力面流体的汇流，产生扩压效应使局部的压力略高。总体来说该透平内温度和压力的变化较连续，没有明显突变区域。

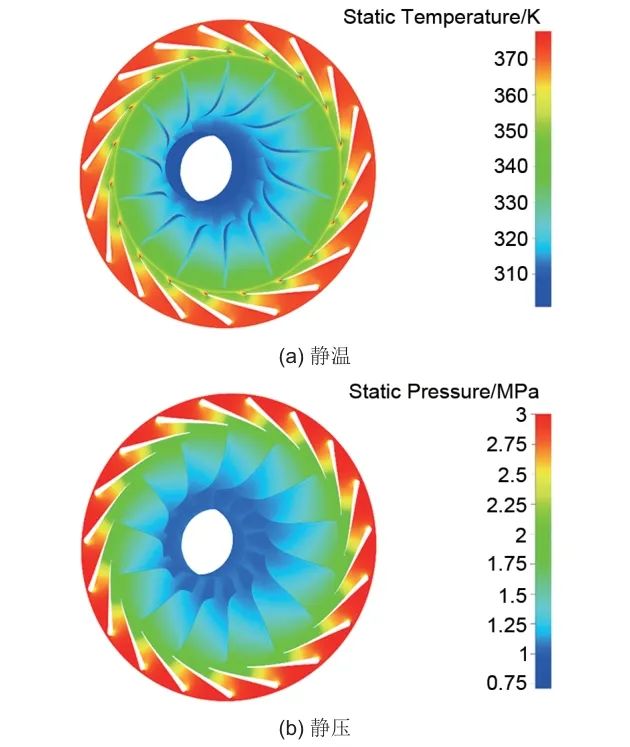
图6   设计工况下透平内静温 (a) 和静压 (b) 分布

喷嘴和叶轮不同叶高处的静压分布如图7所示。由于喷嘴采用的是直叶片，因此喷嘴内的流动较为均匀，不同叶高处的静压分布基本一致，在吸力侧0.2流向位置处，由于流动方向的转变，沿流动方向的面积增加，出现扩压段使得压力略微升高；在喷嘴尾缘处，由于边界层的影响出现了压力波动。叶轮不同叶高处的压力分布存在明显的区别，随着叶片高度的增加，压力面和吸力面的压差总体上是逐渐增加的；而沿着叶片流动方向，吸力面与压力面的压差逐渐减小，在叶轮入口处存在最大的压力差；除叶片尾缘由于尾流涡造成压力波动外，其余位置无明显压力波动。

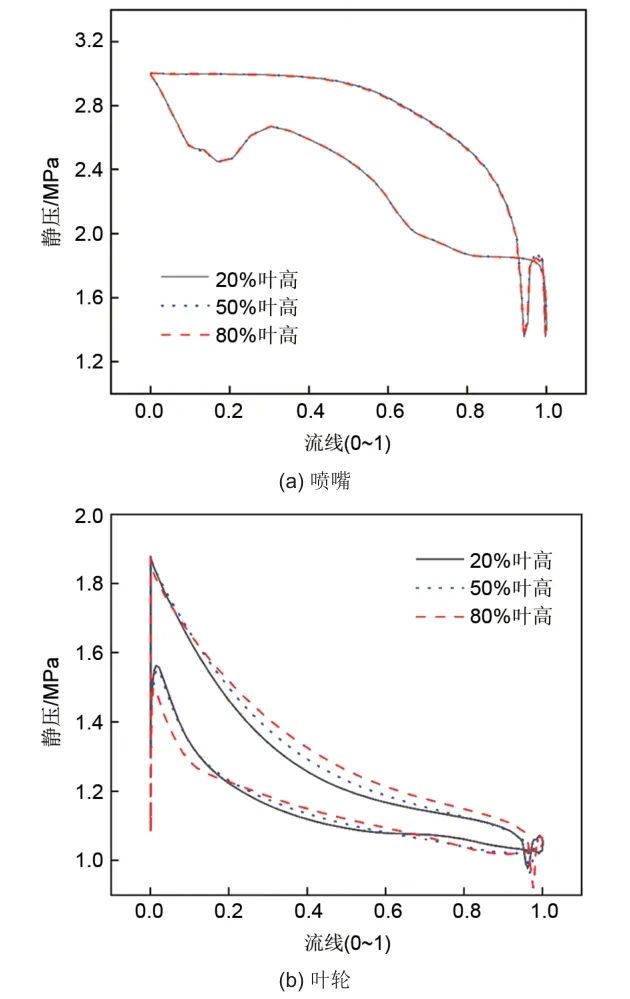
图7   喷嘴 (a) 和叶轮 (b) 不同叶高处的静压分布

二氧化碳储能系统运行工况的变化，会引起透平的运行参数偏离设计值。为保证储能系统的稳定运行，需要对CO2向心透平在非设计工况下的性能进行分析。CO2向心透平变工况分析主要包括变入口压力、变入口温度和变转速，其中变入口压力对于CO2向心透平的质量流量和输出功率影响较大，且向心透平入口压力主要通过影响质量流量的变化来影响输出功率。因此本文保持其他边界条件不变，改变透平入口压力，分析其对该CO2向心透平性能的影响。该CO2向心透平在入口压力低于1.7 MPa或高于12 MPa时，模拟结果不收敛，且变工况分析通常取偏离设计工况±50%的范围，因此入口压力的变化范围取为1.8～4.2 MPa。入口压力对于透平性能的影响如图8所示，当入口压力由1.8 MPa变化到4.2 MPa时，该CO2向心透平的等熵效率先增加后减小，在设计点附近达到最大等熵效率83.51%。对于每个向心透平，存在一个最佳的特性比，当入口压力变化时，特性比偏离最佳值，导致透平等熵效率降低。对于CO2向心透平，更关注其在偏离设计工况±20%范围内的性能变化。该CO2向心透平在偏离设计工况20%(0.6 MPa)的范围内，透平的等熵效率高于82%，表明该透平的变工况性能较好。

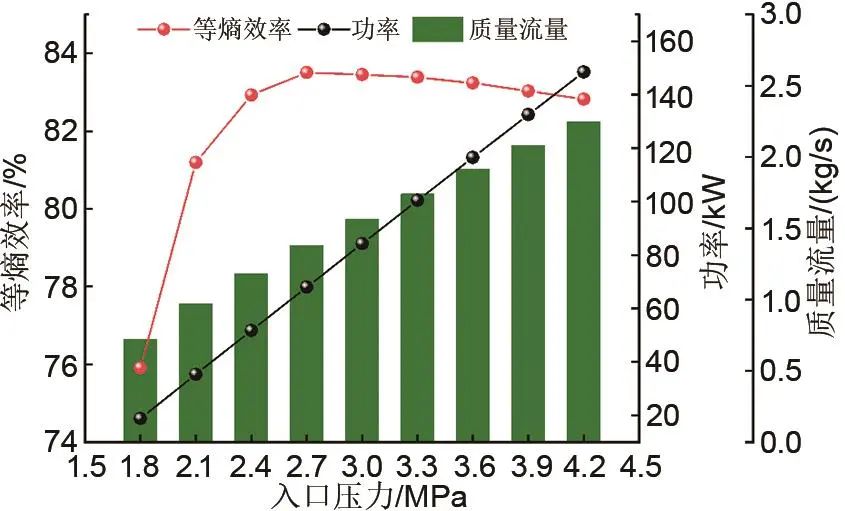
图8   入口压力对于透平性能的影响

随着入口压力的增加，该CO2向心透平的质量流量逐渐增加，且增加的趋势逐渐平缓。入口压力由1.8 MPa变化到4.2 MPa，质量流量由0.724 kg/s增加到2.25 kg/s。该向心透平的通流面积不变，提高入口压力增加了CO2的密度，导致质量流量增加。向心透平流量系数的定义如式(3)所示，在透平压力变化时，流量系数的变化范围为0.46～1.44，与推荐的流量系数调节空间0.4～1.2相接近。入口压力的增加使输出功率由18.84 kW增加到148.48 kW，且变化趋势近似呈线性，入口压力每变化10%(0.3 MPa)，输出功率相应地增加19.2%(16.2 kW)。

表4   入口压力对体积流量的影响

2 向心透平几何结构优化

叶轮的结构直接影响透平的做功能力。叶轮叶片数、叶轮入口角、叶轮出口角、叶顶间隙等几何参数会影响透平内的损失，从而影响透平的性能。叶轮叶片数较多可以降低叶片载荷，优化透平内流场，但是叶片数过多不利于加工，且会增加边界层效应。叶片数较少可以增加通流面积，但会影响流动均匀性。叶轮入口角和叶轮出口角会影响透平流道内漩涡和流动分离区域的面积及位置，进而影响透平效率和输出功率。降低叶顶间隙有助于减小泄漏流，但是叶顶间隙过小会影响透平的安全运行，因此需要分析叶顶间隙与透平效率之间的变化关系。叶轮入口角、叶轮出口角、叶顶间隙如图9所示。

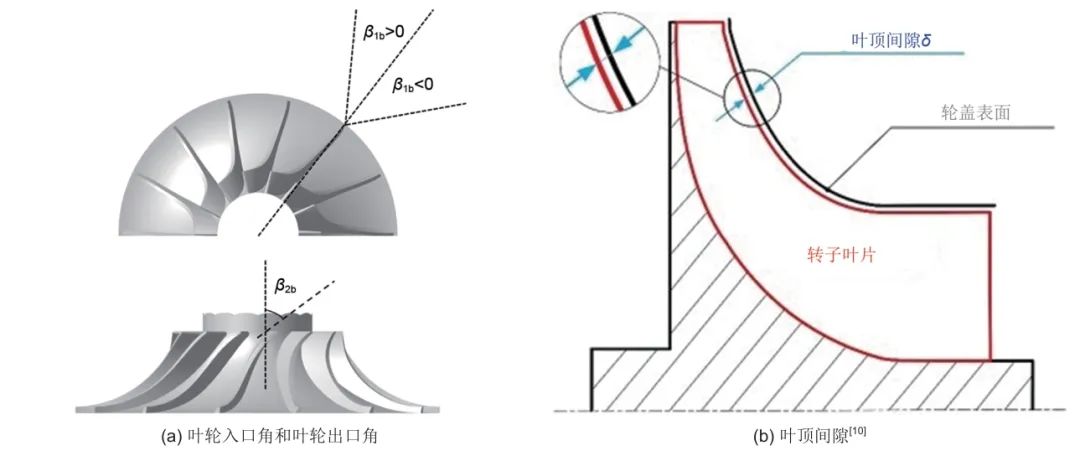
图9   叶轮入口角、叶轮出口角 (a) 和叶顶间隙 (b) 示意图

2.1 叶轮叶片数优化分析

叶轮的叶片数可以根据Glassman经验关系式确定，其表达式如式(4)所示。该CO2向心透平初始叶轮叶片数为14个，另外选取叶轮叶片数为12、13、15、16、17的五种设计作为对比。保持网格数量和边界条件不变，分析叶轮叶片数对于透平性能的影响。图10显示不同叶轮叶片数下透平50%叶高处的马赫数分布，随着叶轮叶片数的增加，流道中的马赫数分布趋于均匀，尾缘的低马赫数区域逐渐缩小，当叶片数达到14个时，流道尾缘的低速区域面积已较小，但是叶片数超过16个后，流道前缘的低马赫数区域增加。过多的叶轮叶片数量会导致流道变窄，增强边界层效应，此外还会增加制造成本，影响系统的经济性。对于该CO2向心透平，14～16个叶轮叶片数比较合适。

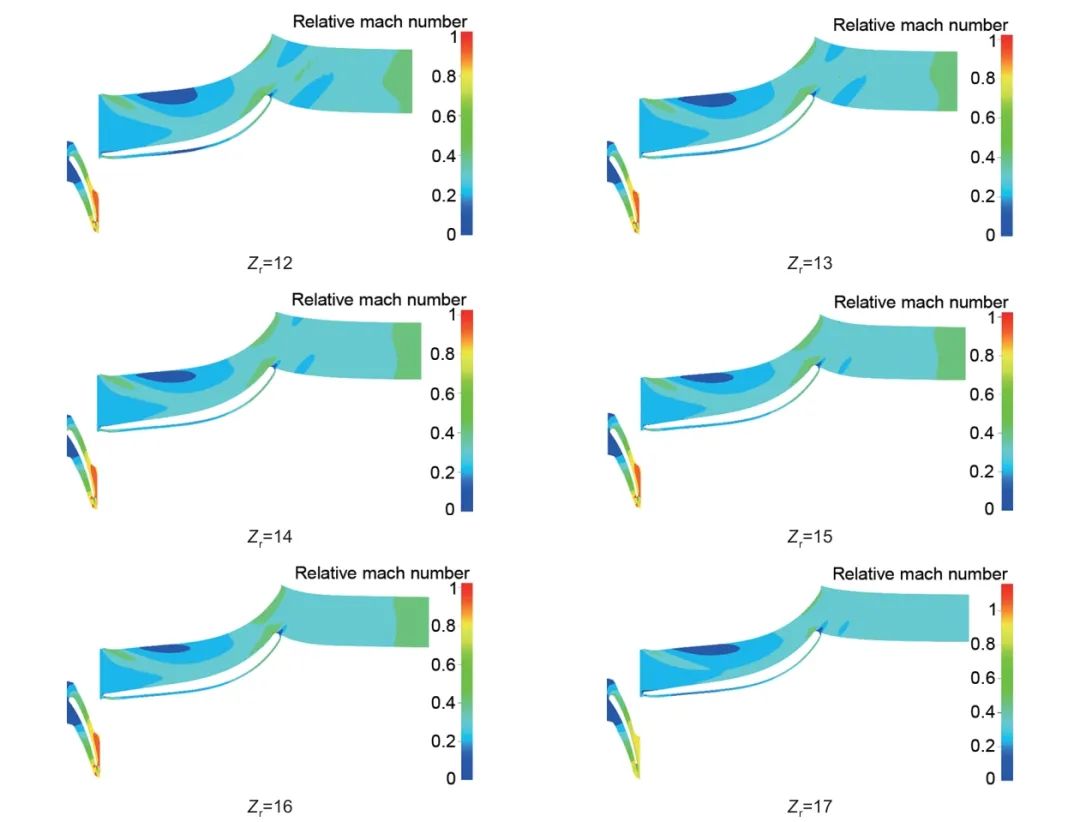
图10   不同叶片数下透平相对马赫数分布

2.2 叶轮入口角优化分析

在叶轮设计时，为使得工质垂直进入叶轮，一般令进口相对速度角和叶轮安装角度相同。但是由于叶轮的旋转以及压力面与吸力面的压力梯度，为使流体更加顺畅地进入叶轮，入射角一般不为零。该CO2向心透平初始叶轮入口角度为0°，在-20°～20°范围内，参照文献[23]中的取值间隔，另取-20°、-10°、10°、20°四组设计作为对照。

图11显示了不同叶轮入口角下CO2向心透平的性能变化，当入口角由-20°变化到20°时，透平的等熵值效率和输出功率均先增加后减小，在叶轮入口角为-10°时透平的等熵效率和输出功率最大，分别为83.07%和84.59 kW。透平出口速度随着叶轮入口角的增加而逐渐增加，但是变化幅度较小。

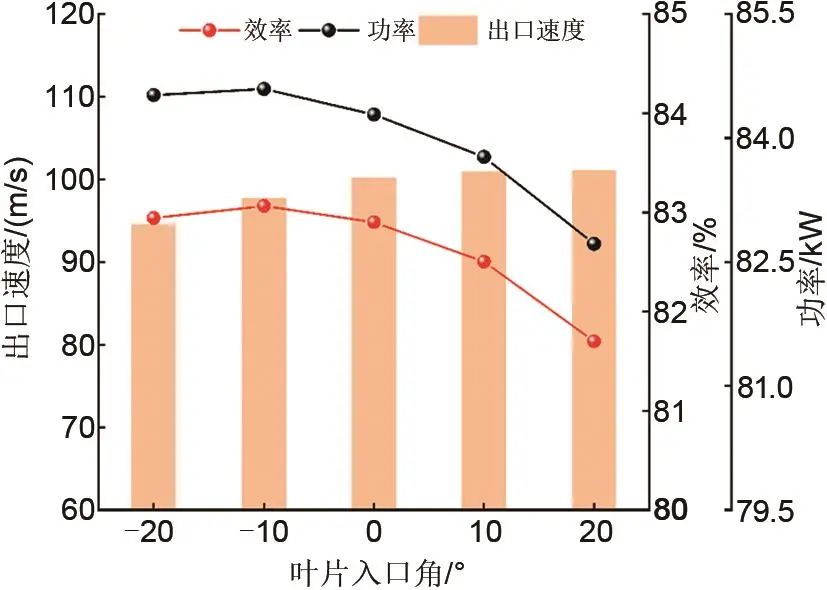
图11   不同叶轮入口角对透平性能的影响

图12表明不同叶轮入口角下CO2透平内的流线分布，在叶片的吸力面存在一个流动分离区域。在-20°时，叶轮入口处还存在小范围低速区域，随着叶轮入口角的增加，入口处的低速区域消失，-10°时吸力面流动分离区域面积与-20°时差异较小。继续增加叶轮入口角，流动分离区域的面积逐渐增加，且流动分离区域逐渐向下游移动，在20°时，流动分离区域已经从叶轮流道的前缘移动到流道中部区域。

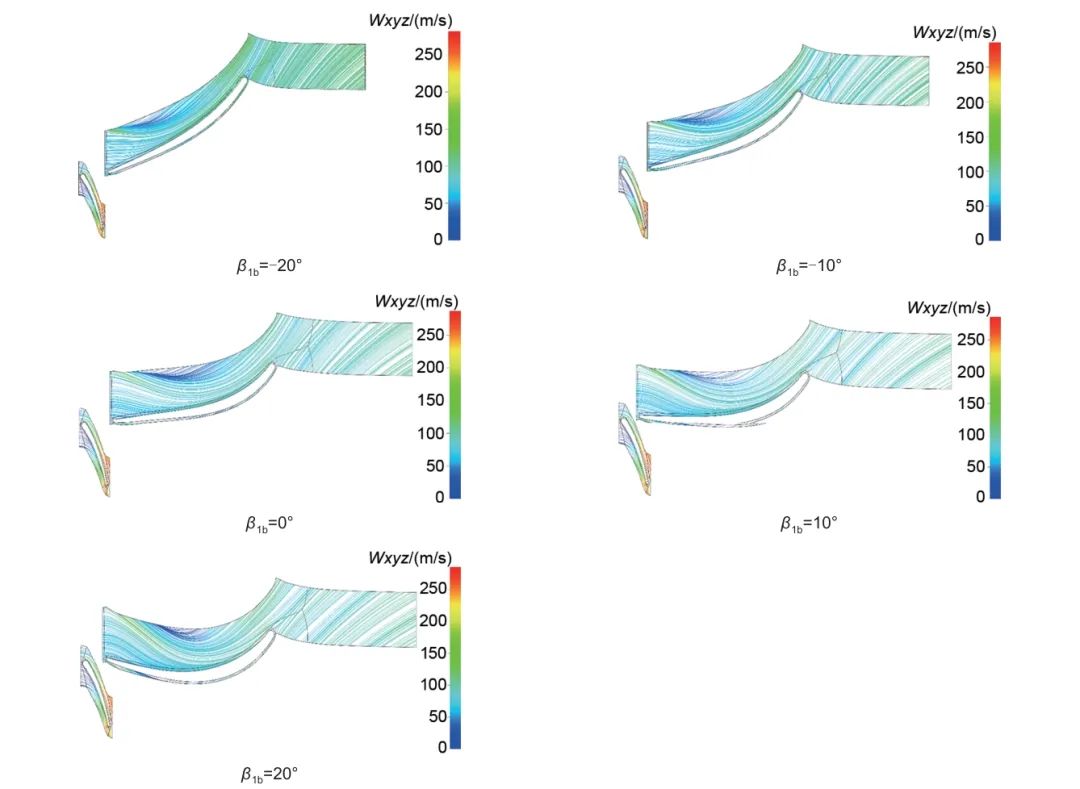
图12   不同叶轮入口角下透平流线分布

在叶轮损失中占比较大的是间隙损失、流道损失和余速损失，占叶轮损失的90%左右。在叶轮叶顶间隙不变时，可以认为间隙损失基本不变。CO2透平出口速度的变化较小，可以忽略余速损失变化对于透平效率的影响。因此在叶轮入口角变化时，流道损失的变化占据主要地位，此时透平内的流道损失先减小后增大，在-10°时流道损失最小，过大或过小的叶轮入口角都会增加吸力面的流道损失。因此-10°可认为是该CO2向心透平的最佳入口角，该数值与理论结果接近。

2.3 叶轮出口角优化分析

叶轮出口角决定了工质的膨胀流动和出口速度大小，合适的叶轮出口角可以降低流动分离。叶轮入口角取为-10°，改变叶轮出口角，分析其对透平性能的影响。叶轮出口角的初始值为-63°，考虑叶片几何结构的限制，叶轮出口角度最大值约为-82°。因此选取-53°、-73°、-82°三组作为对照。

不同叶轮出口角下透平性能对比如表5所示，随着叶轮出口角变化，透平效率先增加后降低，在-73°时透平的等熵效率最大为83.65%。在-82°时流动出现堵塞，透平质量流量和功率变为1.506 kg/s和80.85 kW，较初始设计降低了3.65%和4.07%。

表5   不同叶轮出口角下透平性能对比

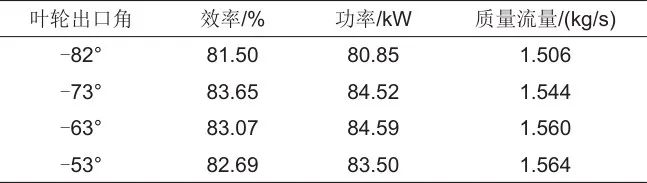
不同叶轮出口角下20%叶高处的流线分布如图13所示，当叶轮出口角由-82°变化到-53°时，叶片吸力面的涡尺度逐渐减小，叶轮出口相对速度逐渐减小，叶轮出口处的流动逐渐恶化且涡面积逐渐增加，在-53°时可以在叶轮出口处观察到明显的涡分布。50%叶高处的流线分布如图14所示，叶片吸力面均有涡分布，且随着叶轮出口角的增加，叶轮出口处的涡面积逐渐扩大。80%叶高处的流线分布如图15所示，叶轮出口处的涡不明显，但叶轮吸力面涡分布较叶根和叶中处的明显。因此对于该CO2向心透平，叶轮出口处的涡分布主要集中在叶根和叶中处，吸力面处的涡分布主要集中在叶顶处。随着叶轮出口角变化，总的涡损失先减小后增加，在-73°时透平性能最优。

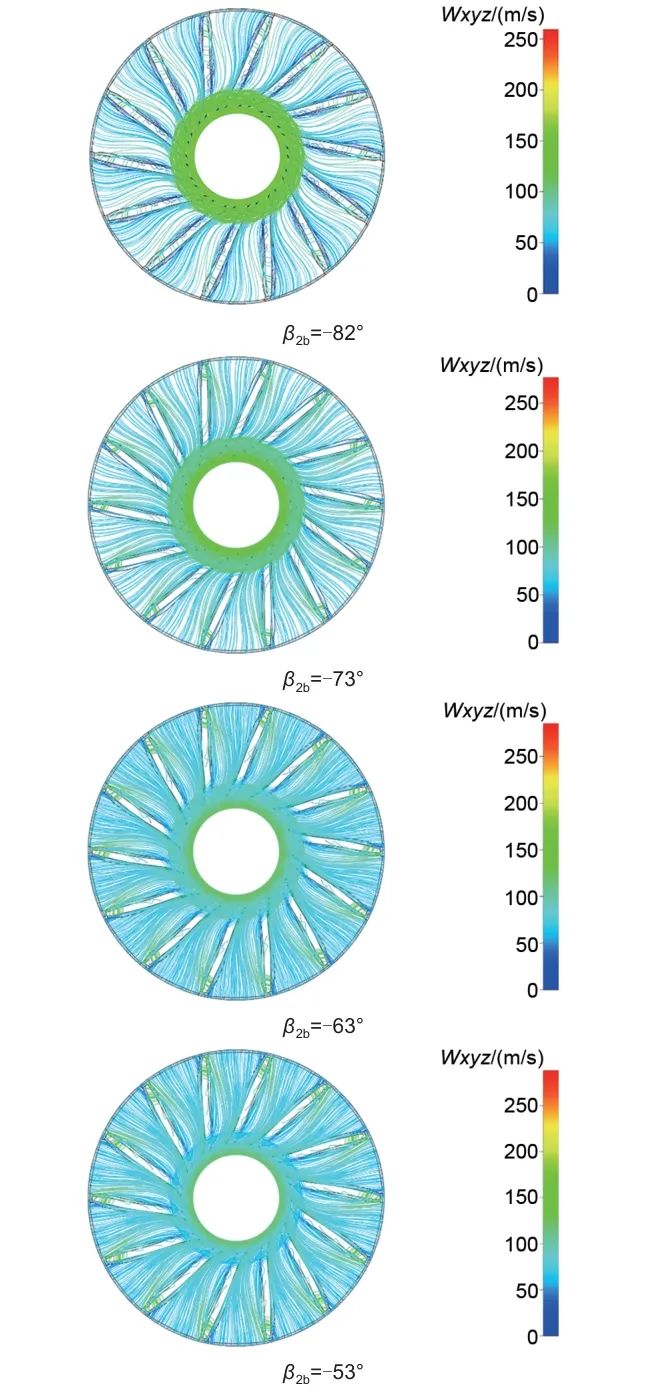
图13   20%叶高处流线图

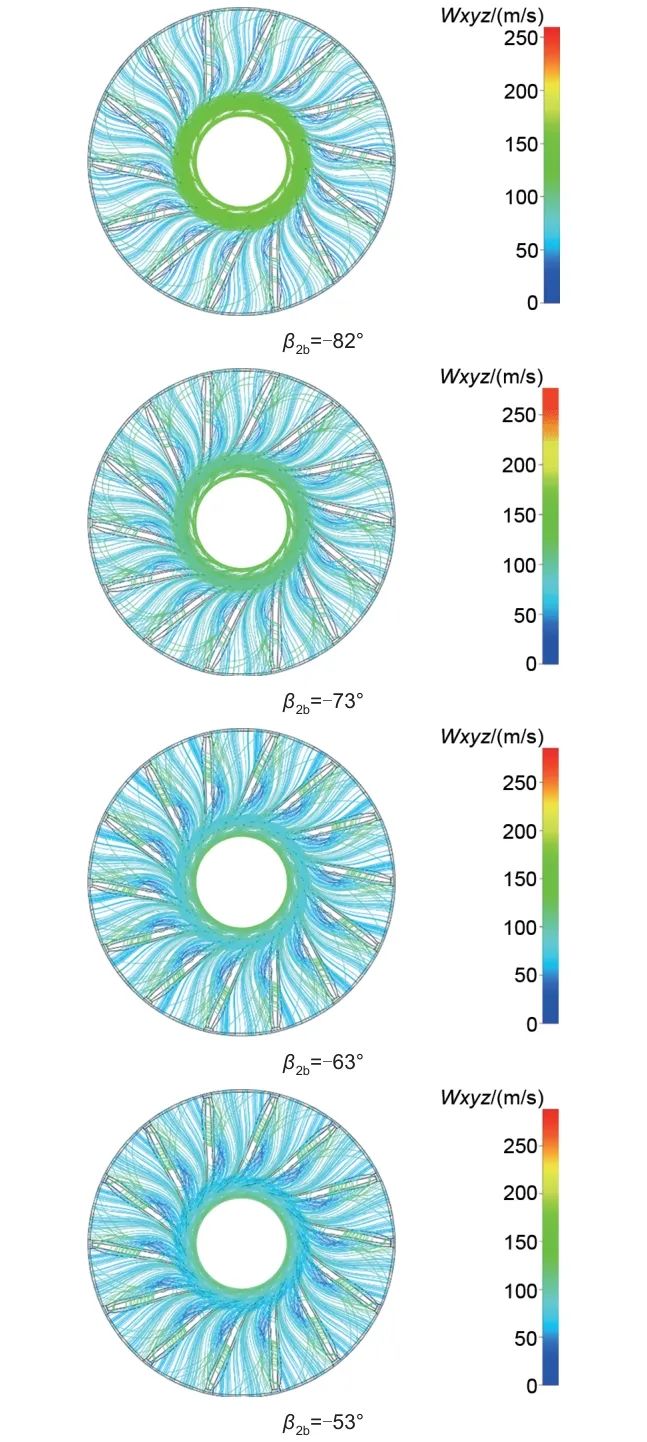
图14   50%叶高处流线图

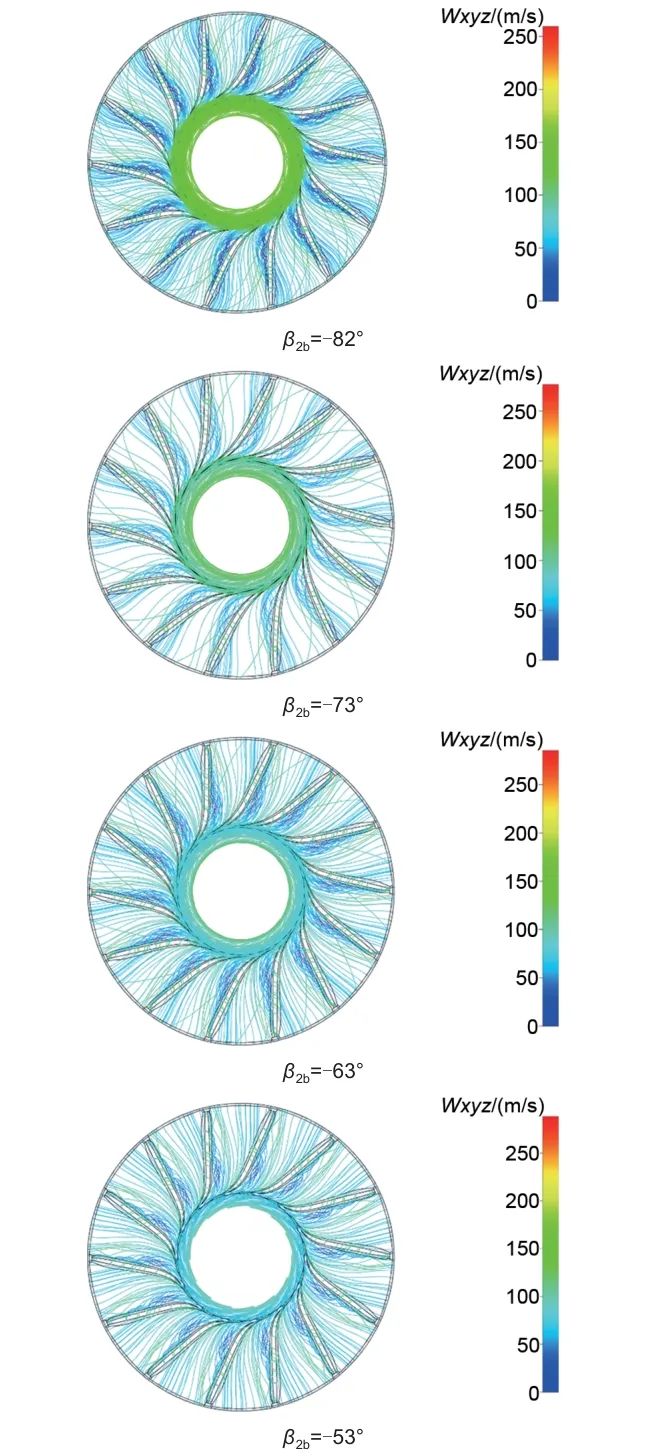
图15   80%叶高处流线图

优化叶轮入口角和出口角后，该CO2向心透平在设计点的等熵效率较初始设计提升了0.75%。为详细分析该透平的性能变化，需要对非设计工况进行验证。采用与原设计相同的变工况模拟，入口压力由1.8 MPa增加到4.2 MPa，其他边界条件保持不变。优化后透平的等熵效率变化如图16所示。除了高膨胀比工况外，优化后CO2向心透平等熵效率得到提升，且在低膨胀比工况下透平等熵效率的提高幅度在0.31%～1.02%之间，有利于二氧化碳储能系统在高压储罐压力降低的情况下稳定运行。

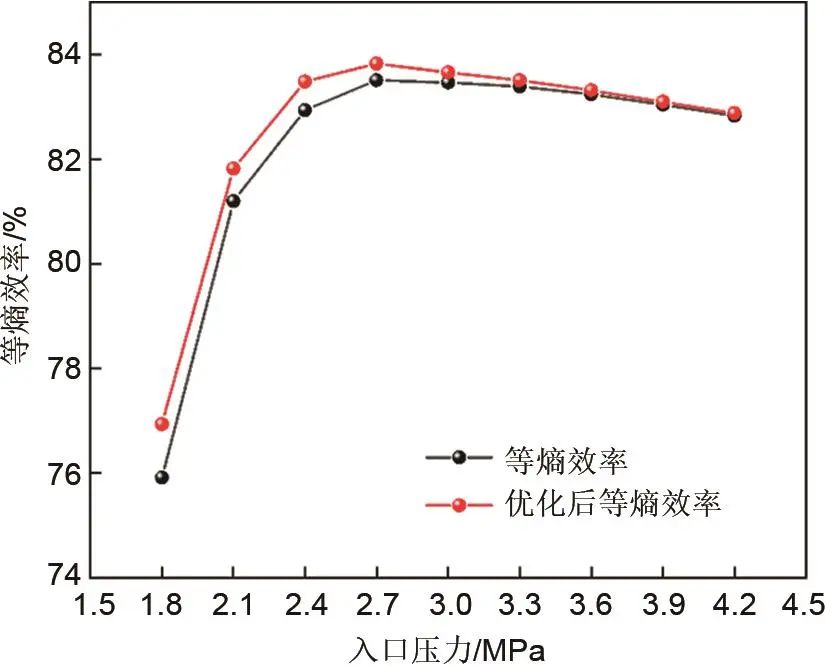
图16   优化前后CO2向心透平效率对比

3 叶顶间隙分析

为保证CO2向心透平的安全运行，需要在叶轮叶片顶部与轮盖之间保留间隙，但间隙的增加会造成透平性能的下降。对SCO2向心透平和有机工质向心透平叶顶间隙的研究表明，当叶顶间隙每增加1%，透平效率相对降低0.64%和0.53%。参考SCO2向心透平叶顶间隙的取值，该透平的叶顶间隙分别取为0.1 mm、0.2 mm、0.3 mm、0.4 mm、0.5 mm，并与无叶顶间隙的工况进行对比。

不同叶顶间隙对于透平效率的影响如图17所示，当叶顶间隙从0增加到0.5 mm，叶顶间隙与叶轮叶高的比值从0%增加到20.4%，CO2向心透平的效率由88.04%降低到79.89%，该向心透平效率随着叶顶间隙的增加而线性递减。叶顶间隙每增加1%，透平效率相对降低0.40%。

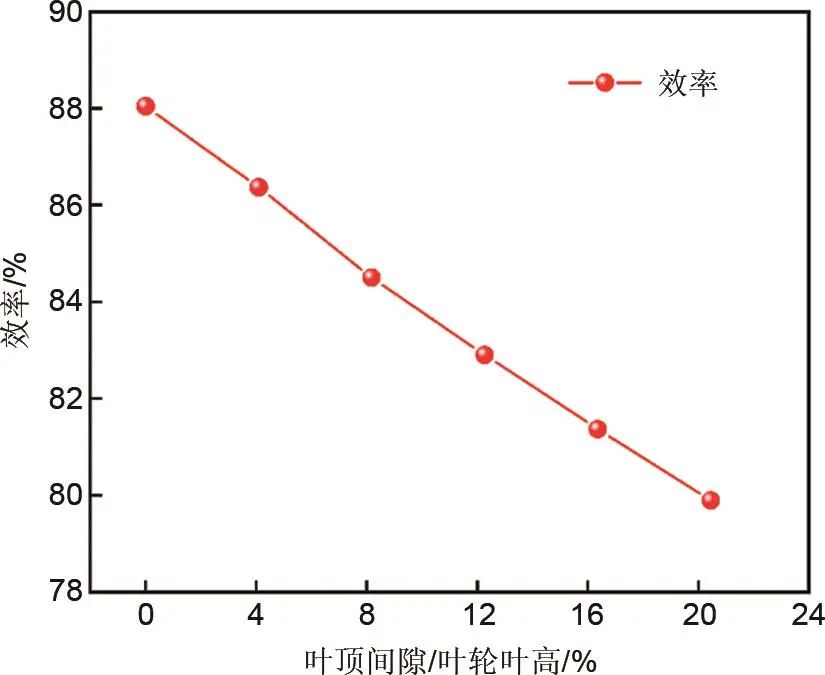
图17   叶顶间隙对于透平性能的影响

不同叶顶间隙下，垂直于叶片的截面流线分布如图18所示。随着叶顶间隙的增加，压力面与吸力面之间的泄漏量增加且压力梯度逐渐缩小。此外吸力面的泄漏涡面积逐渐增加，在叶顶间隙为0.1 mm时泄漏涡分布不明显，当叶顶间隙为0.4 mm、0.5 mm时，可以观察到明显的泄漏涡分布，且泄漏涡距离吸力面的距离随着间隙的增加而增加。不同叶顶间隙下叶轮内的流线分布如图19所示。随着叶顶间隙的增加，泄漏流的流速及其所占流道面积均增加，泄漏流对于主流的阻碍作用更加明显。主流由于泄漏流而产生偏转，使得叶轮不能很好地引导流动方向，因此透平内的损失增加。

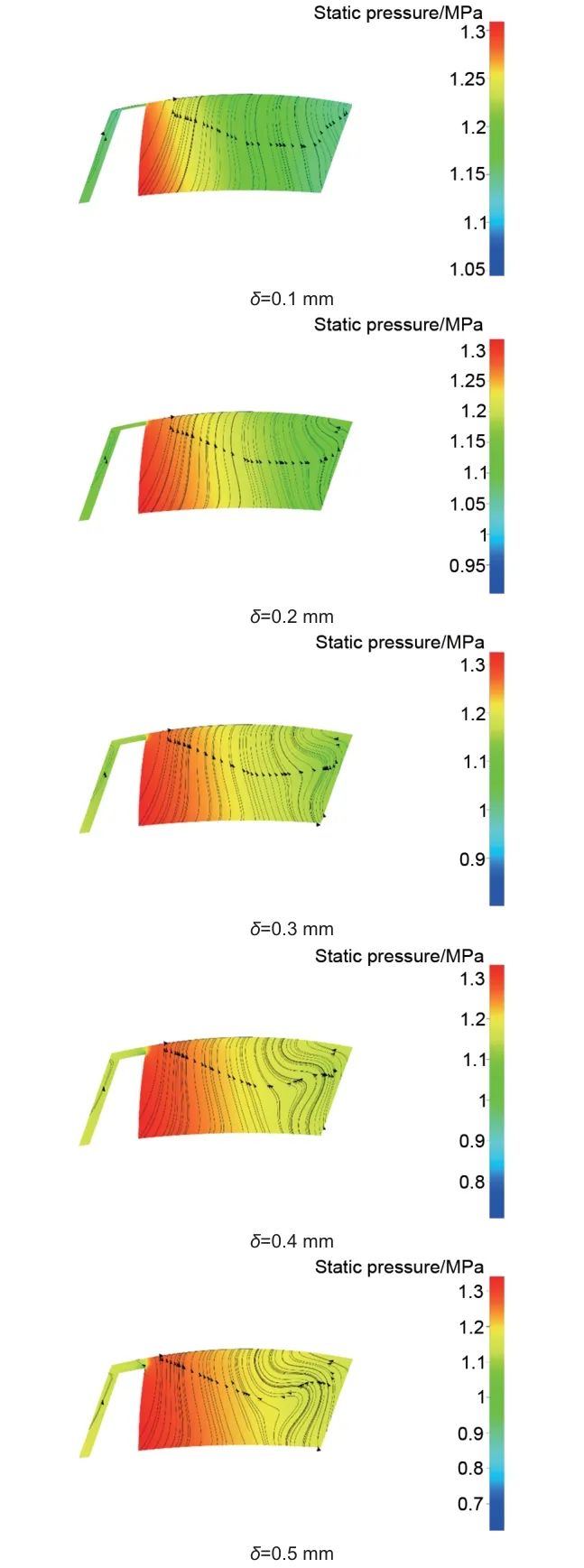
图18   不同叶顶间隙下截面的流线分布

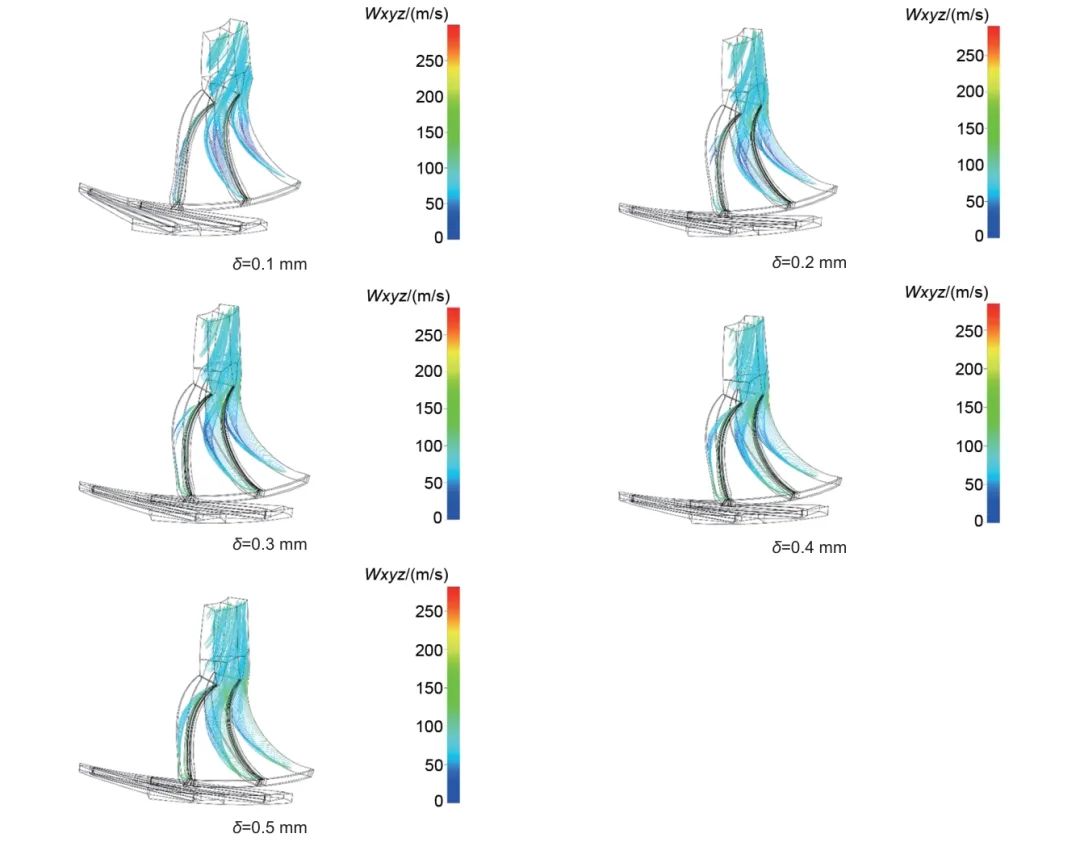
图19   不同叶顶间隙下叶轮内的流线分布

4 向心透平非定常流动分析

由于喷嘴和叶轮叶片具有相对运动，透平内流场具有明显的非定常特性，进而影响下游叶片的干涉和二次流输运，且非定常计算可捕捉到更为细致的流场结构。Numeca中的非定常分析方法包括全三维黏性非定常模拟和非线性谐波法(NLH)，其中NLH方法假设非定常流动是由时均流动和若干扰动叠加而成，可以在占用较少计算资源的前提下模拟动静叶片的非定常流动效应，且喷嘴和叶轮流道内的流动具有周期性，因此可以用谐波函数来逼近。本文分别采用两种方法对透平进行非定常分析，并与稳态分析结果进行对比。

NLH模拟与定常模拟的结果对比如表6所示，考虑非定常效应的影响，透平效率降低0.23%，功率和质量流量略有下降。采用熵产方法可以揭示非定常相互作用的机理，不同时刻的熵值分布如图20所示，喷嘴区域的熵产较低，高熵产区域主要集中在叶轮吸力面前缘及其流道中后部，喷嘴尾迹流呈现周期性变化。喷嘴尾迹流在叶片前缘被分割，且由于吸力面与压力面的流速不同，尾迹流在剪切作用下形成片段，沿着压力面和吸力面向下游传播，从而引起下游流道的熵值变化。

表6   NLH模拟和定常模拟的对比

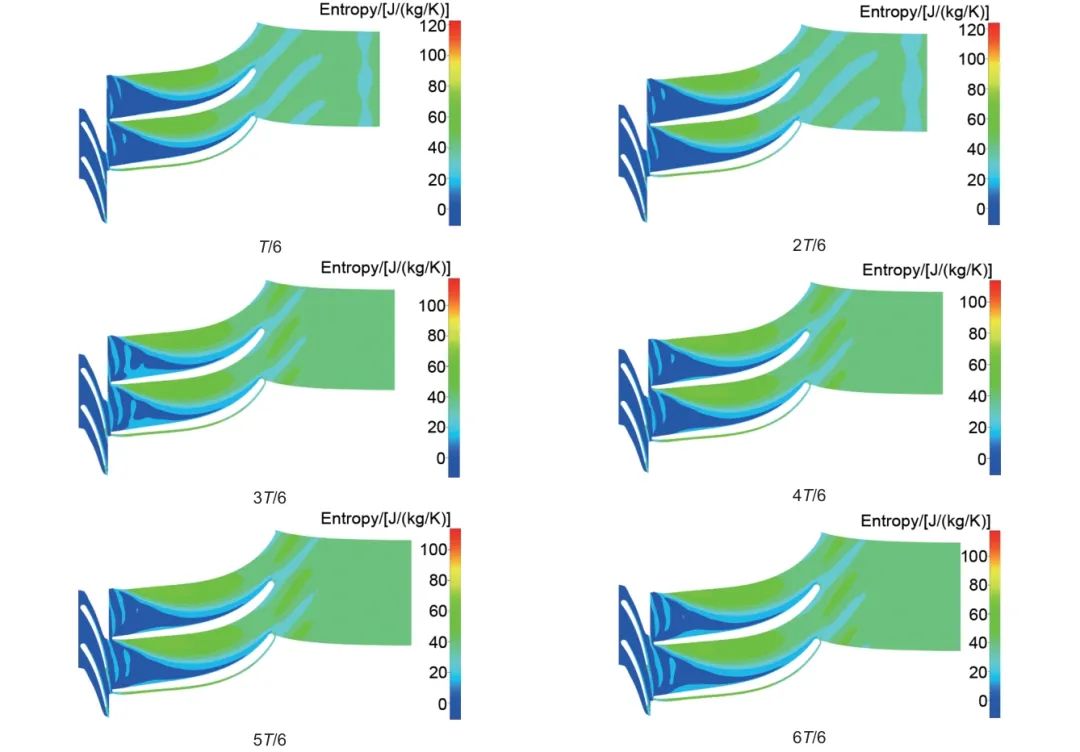
图20   NLH模拟不同时刻熵值分布

采用全三维黏性非定常模拟时，要求喷嘴和叶轮交界面的上下游具有相同的周期性。因此通过叶片数约化或几何缩放，改变叶片的数量以便在较少叶片通道计算域下直接利用周期性边界，有助于减少计算量。将喷嘴叶片数由19个调整到21个，动静叶片数比变为2∶3，此时计算域中包括3个喷嘴流道和2个叶轮流道。为排除喷嘴叶片数量的调整对计算结果的影响，利用NLH方法对改变叶片数的透平进行计算，全三维黏性非定常模拟、NLH模拟与定常模拟结果如表7所示。NLH方法模拟的效率较定常值下降了0.14%，与不调整喷嘴叶片数量时的结果相接近。全三维黏性非定常模拟的效率较定常值下降了0.57%，其技术结果较NLH方法更准确，可见相较于喷嘴叶片数量的变化，非定常流动对于透平性能的影响较大。不同时刻透平内熵值分布如图21所示。其熵值分布与NLH方法得到的结果类似，喷嘴尾迹流造成叶轮内的非定常流动，其在叶轮前缘分离成片段并沿着流道向下游传播，总体呈周期性变化。对比两种非定常分析的计算结果与流场分布，全三维黏性非定常模拟的计算结果更准确，但NLH方法也可以捕捉到喷嘴的尾迹流，可用于粗略分析动静叶片的非定常干涉效应。

表7   全三维黏性非定常模拟、NLH模拟和定常模拟的对比

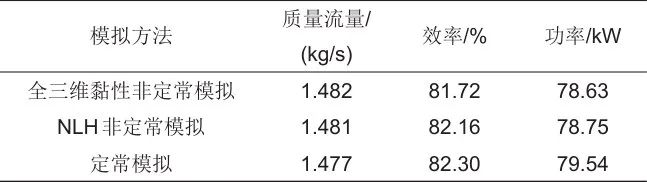
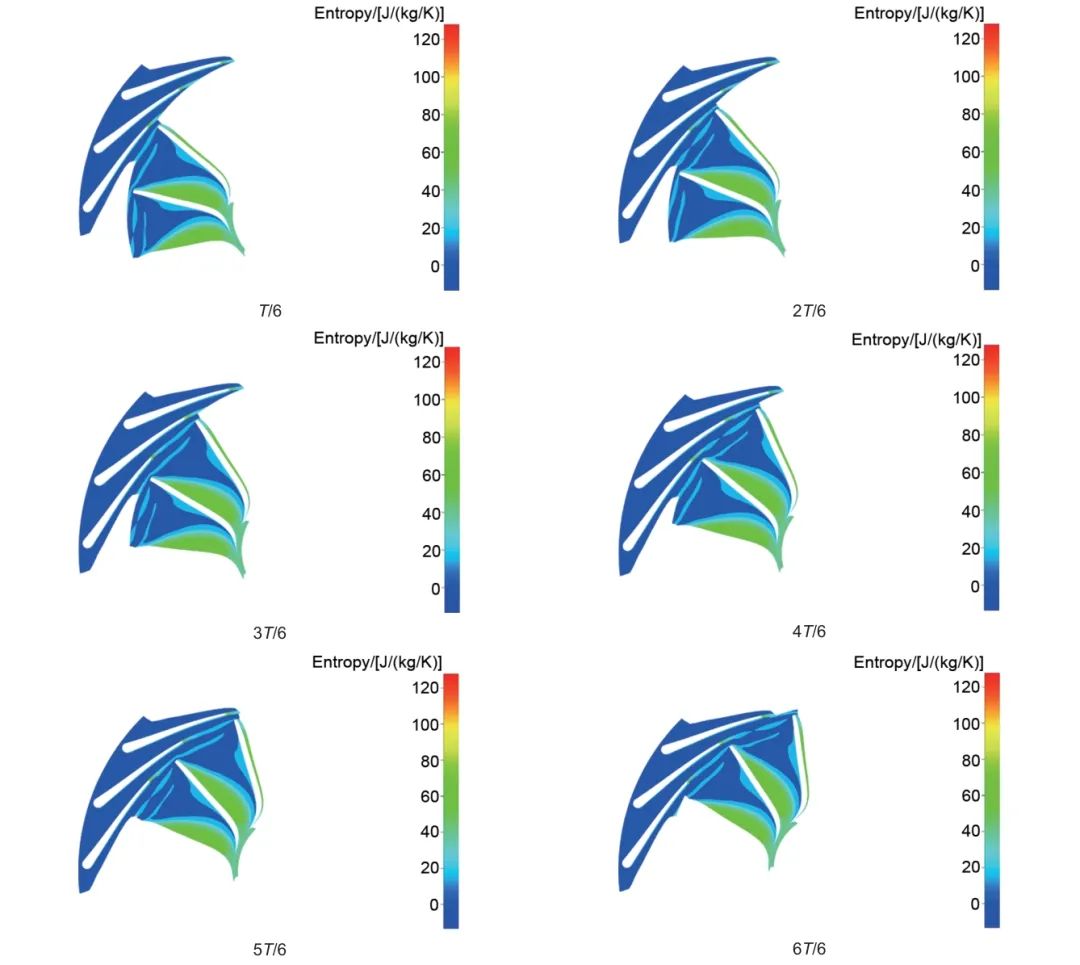
图21   全三维黏性非定常模拟不同时刻的熵值分布

5 结论及展望

本文通过对某百千瓦级二氧化碳储能系统向心透平进行设计和多流场分析，探究了叶轮叶片数、叶轮入口角、叶轮出口角、叶顶间隙等结构参数对于透平流动特性的影响，进一步分析了非定常流动下透平内的流场分布，主要结论如下：

（1）模拟结果与一维设计结果的最大偏差为4.15%，表明该设计方法较为合理。在设计工况下，该CO2透平的等熵效率为82.90%，输出功率为84.28 kW，质量流量为1.563 kg/s，均满足设计要求。透平内的流线分布较连续，无明显的速度突变。在偏离入口压力20%的范围内，透平的等熵效率高于82%，表明该透平的变工况性能较好。

（2）叶轮叶片数、叶轮入口角、叶轮出口角会影响透平的性能。随着叶轮叶片数的增加，流道尾缘的低马赫数区域逐渐缩小，但是当叶轮叶片数过多时，流道前缘的低马赫数区域增加。对于该透平，14～16个叶轮叶片数比较合适。叶轮入口角通过影响流道损失来影响透平的效率，随着叶轮入口角的变化，叶轮吸力面的流道损失先减小后增大。叶轮出口角会影响叶轮吸力面和出口处的涡量分布，且吸力面处的涡主要集中在叶顶处，叶轮出口处的涡主要集中在叶根和叶中处。

（3）优化后叶轮入口角为-10°，叶轮出口角为-73°。优化叶轮角后，该CO2向心透平在设计点的等熵效率为83.65%，较初始设计提高了0.75%。改变透平入口压力，除高膨胀比工况外，该CO2向心透平的性能得到提升。叶顶间隙的增加导致压力面与吸力面的泄漏量增加，泄漏涡的面积亦随之增加。透平效率随着叶顶间隙的增加而线性递减，叶顶间隙每增加1%，透平效率相对降低0.40%。

（4）在非定常流动分析下，喷嘴尾迹流呈现周期性变化，在剪切作用下，沿着压力面和吸力面向下游传播，引起下游流道内熵值的变化。采用全三维黏性非定常模拟时，等熵效率较定常时下降了0.57%。非定常流动对于透平效率的影响较大，采用NLH方法时，透平效率较定常时降低0.23%。NLH方法也可捕捉到动静叶片的干涉效应，因此可用于粗略分析非定常流动的影响。

本研究对二氧化碳储能系统中向心透平进行了优化设计开发，然而实际运行过程中的透平损失变化也是评价透平性能的重要环节，这部分工作将在后续展开。此外，系统规模放大后对透平亦提出新要求，大流量、多段多级、补气调节等也是重要的研究内容。